Locus van punten - deze set allemaal punten, voldoen aangegeven bepaalde voorwaarden.

VOORBEELD 1. De mediaanloodlijn van elk segment is een geometrische

plaats van punten (d.w.z. de verzameling van alle punten), op gelijke afstandvan

uiteinden van dit segment. Laat PO AB en AO = OB:

Dan zijn de afstanden van elk punt P dat op de middelloodlijn PO ligt tot de uiteinden A en B van het segment AB gelijk en gelijk aan D.

Op deze manier, elk punt van de mediaanloodlijn segment heeft de volgende eigenschap: het is op gelijke afstand van de uiteinden van het segment.

VOORBEELD 2. bissectrice hoeker ismeetkundige plaats van punten op gelijke afstand van zijn zijden.

VOORBEELD 3. De cirkel is de verzameling punten (d.w.z. de verzamelingstvo

alle punten) gelijke afstand vanuit het centrum(de afbeelding toont er een)

Vanaf deze punten - A).

Cirkel - het locus van punten (d.w.z. de verzameling van alle punten) in het vlak,gelijke afstandvanaf één punt het middelpunt van de cirkel genoemd. Een lijnstuk dat het middelpunt van de cirkel verbindt met een willekeurig punt erop heet straal en aangegeven R of R. Het deel van het vlak dat wordt begrensd door een cirkel heet rondom. Deel van een cirkel (A m B, fig.39) heet boog. De lijn PQ die door de punten M en N van de cirkel gaat (Fig. 39) heet secans, en zijn segment MN, dat binnen de cirkel ligt - akkoord.

Een akkoord dat door het middelpunt van een cirkel gaat (bijvoorbeeld BC, Fig. 39) wordt genoemd diameter en aangegeven D of D. Diameter is het grootste akkoord gelijk aan twee stralen ( D= 2 R).

Raaklijn. Stel dat de secans PQ (Fig. 40) door de punten K en M van de cirkel gaat. Laten we ook aannemen dat het punt M langs de cirkel beweegt en het punt K nadert. Dan zal de secans PQ van positie veranderen en rond het punt K draaien. Als het punt M het punt K nadert, zal de secans PQ tot een bepaalde limiet neigen positie AB. De lijn AB heet raaklijn naar de cirkel in het punt K. Het punt K heet aanraakpunt. De raaklijn en de cirkel hebben maar één gemeenschappelijk punt - het contactpunt.

Lesdoelen:

• Educatief: laat een nieuwe methode zien voor het oplossen van problemen voor het construeren van de puntenverzameling; Leer hoe u het kunt gebruiken om problemen op te lossen.
• Ontwikkelen: ontwikkeling van het visueel-figuratief denken; cognitieve interesse.
• Educatief: ontwikkeling van het vermogen om werk te plannen, te zoeken naar rationele manieren om het uit te voeren, het vermogen om met reden een mening te verdedigen en het resultaat kritisch te evalueren.

Lesdoelen:

• Nieuwe stof leren.
• Controleer het vermogen van de leerlingen om problemen op te lossen.

Lesplan:

1. definities.
2. voorbeeld 1
3. Voorbeeld 2
4. Voorbeeld 3
5. Theoretisch gedeelte.
6. Algemene concepten.

Invoering.

De oude Egyptische en Babylonische cultuur op het gebied van wiskunde werd door de Grieken voortgezet. Ze beheersten niet alleen alle ervaring van hun geometrie, maar gingen ook veel verder. Wetenschappers van het oude Griekenland waren in staat om de verzamelde geometrische kennis in een systeem te brengen en zo de basis te leggen voor geometrie als een deductieve wetenschap.

Bij het aanleggen van handelsroutes maakten Griekse kooplieden kennis met oosterse wiskunde. Maar de mensen in het Oosten hadden weinig met theorie te maken, en de Grieken ontdekten dit snel. Ze stelden vragen: waarom zijn in een gelijkbenige driehoek twee hoeken aan de basis gelijk; Waarom is de oppervlakte van een driehoek gelijk aan de helft van de oppervlakte van een rechthoek met dezelfde basis en hoogte?

Helaas zijn er geen primaire bronnen die de vroege ontwikkelingsperiode van de Griekse wiskunde beschrijven. Alleen dankzij de gerestaureerde teksten uit de vierde eeuw voor Christus en het werk van Arabische geleerden, die rijk waren aan vertalingen van de geschriften van de auteurs van het oude Griekenland, hebben we edities van Euclides, Archimedes, Apollonius en andere grote mensen. Maar in deze werken is al een volledig ontwikkelde wiskundige wetenschap vertegenwoordigd.

De wiskunde van het oude Griekenland heeft een lang en complex ontwikkelingspad doorlopen, te beginnen vanaf de 6e eeuw voor Christus. en tot de 6e eeuw. Wetenschapshistorici onderscheiden drie perioden van haar ontwikkeling in overeenstemming met de aard van kennis:

1. Accumulatie van individuele wiskundige feiten en problemen (6 - 5B.B. BC).
2. Systematisering van opgedane kennis (4e - 3e eeuw v. Chr.).
3. De periode van computationele wiskunde (3e eeuw voor Christus - 6e eeuw).

Geometrische puntenverzameling (GMT).

definities.

geometrische plaats- een term die in de oude literatuur over meetkunde werd gebruikt en nog steeds wordt gebruikt in de onderwijsliteratuur, om te verwijzen naar reeksen punten die aan een bepaalde voorwaarde voldoen zijn meestal geometrisch. Bijvoorbeeld: de meetkundige plaats van punten op gelijke afstand van twee gegeven punten A en B is de middelloodlijn op segment AB. Soms hebben ze het ook over de plaats van lijnen en andere figuren.

De naam wordt geassocieerd met het concept van een lijn als een "plaats" waar punten zich bevinden.

In geometrie, het traject van een bepaald punt dat beweegt in overeenstemming met een bepaalde formule of voorwaarde. Een cirkel is bijvoorbeeld de meetkundige plaats van een punt dat zich op een vlak beweegt, zodat de afstand van zijn locatie tot het middelpunt ongewijzigd blijft.

Locus van punten (LTP)- dit is een reeks punten, die alle punten omvat die aan een bepaalde voorwaarde voldoen, en alleen zij.

Locus van punten (LTP)- een stijlfiguur in de wiskunde die wordt gebruikt om een ​​geometrische figuur te definiëren als een reeks punten die een bepaalde eigenschap hebben.

Voorbeelden.

• De middelloodlijn van een segment is de meetkundige plaats van punten op gelijke afstand van de uiteinden van het segment.
• Een cirkel is de verzameling punten op gelijke afstand van een bepaald punt, het middelpunt van de cirkel genoemd.
• Een parabool is de verzameling punten op gelijke afstand van een punt (de focus genoemd) en een rechte lijn (de richtlijn genoemd).

voorbeeld 1

De mediaanloodlijn van elk segment is de meetkundige plaats van punten (d.w.z. de verzameling van alle punten) op gelijke afstand van de uiteinden van dit segment. Laat PO loodrecht op AB staan ​​en AO = OB:

Dan zijn de afstanden van elk punt P dat op de mediaan loodrecht PO ligt tot de uiteinden A en B van het segment AB hetzelfde en gelijk aan d .

Elk punt van de mediaanloodlijn van het segment heeft dus de volgende eigenschap: het ligt op gelijke afstand van de uiteinden van het segment.

Voorbeeld 2

De bissectrice van een hoek is de verzameling punten op gelijke afstand van zijn zijden.

Voorbeeld 3

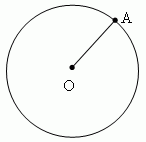
De cirkel is de verzameling punten (d.w.z. de verzameling van alle punten) op gelijke afstand van het middelpunt (de afbeelding toont een van deze punten - A).

Akkoord, die door het middelpunt van de cirkel gaat (bijvoorbeeld BC, figuur 1), wordt de diameter genoemd en wordt aangeduid met d of D. Diameter is het grootste akkoord gelijk aan twee stralen (d = 2 r).

Raaklijn. Stel dat de secans PQ (Fig. 2) door de punten K en M van de cirkel gaat. Laten we ook aannemen dat het punt M langs de cirkel beweegt en het punt K nadert. Dan zal de secans PQ van positie veranderen en rond het punt K draaien. Als het punt M het punt K nadert, zal de secans PQ tot een bepaalde limiet neigen positie AB. De lijn AB wordt de raaklijn aan de cirkel in het punt K genoemd. Het punt K wordt het raakpunt genoemd. De raaklijn en de cirkel hebben maar één gemeenschappelijk punt - het contactpunt.

Tangent eigenschappen.

1. De raaklijn aan de cirkel staat loodrecht op de straal getrokken naar het contactpunt (AB staat loodrecht op OK, Fig. 2).
2. Vanaf een punt buiten de cirkel kunnen twee raaklijnen aan dezelfde cirkel worden getrokken; hun segmenten zijn gelijk aan AB=AC (Fig. 3).

Segment- dit is het deel van de cirkel dat wordt begrensd door de boog ACB en het bijbehorende akkoord AB (Fig. 4). De lengte van de loodrechte CD getrokken vanaf het midden van de koorde AB tot het snijpunt met de boog ACB wordt de hoogte van het segment genoemd.

Hoeken in een cirkel.

Centrale hoek - de hoek gevormd door twee stralen (∠AOB, Fig.5). Een ingeschreven hoek is een hoek gevormd door twee koorden AB en AC getrokken uit hun gemeenschappelijk punt (∠BAC, Fig.4). De beschreven hoek is de hoek gevormd door twee raaklijnen AB en AC getrokken vanuit één gemeenschappelijk punt (∠BAC, Fig.3).

Relaties tussen de elementen van de cirkel.

Ingeschreven hoek(∠ABC, Fig.7) is gelijk aan de helft van de centrale hoek op basis van dezelfde boog AmC (∠AOC, Fig.7). Daarom zijn alle ingeschreven hoeken (Fig. 7) gebaseerd op dezelfde boog (AmC, Fig. 7) gelijk. En aangezien de centrale hoek hetzelfde aantal graden bevat als zijn boog (AmC, Fig. 7), wordt elke ingeschreven hoek gemeten door de helft van de boog waarop hij rust (in ons geval AmC).

Alle ingeschreven hoeken op basis van een halve cirkel (∠APB, ∠AQB, ..., Fig. 8) zijn recht.

Injectie(∠AOD, Fig.9), gevormd door twee akkoorden (AB en CD), wordt gemeten door de helft van de som van de bogen tussen de zijkanten: (AnD + CmB) / 2 .

De hoek (∠AOD, Fig. 10) gevormd door twee snijvlakken (AO en OD) wordt gemeten door het halve verschil van de bogen tussen de zijden: (AnD - BmC) / 2.

De hoek (∠DCB, Fig. 11) gevormd door de raaklijn en de koorde (AB en CD) wordt gemeten door de halve boog die erin zit: CmD / 2.

De hoek (∠BOC, Fig.12) gevormd door de raaklijn en de secans (CO en BO) wordt gemeten door het halve verschil van de bogen die tussen de zijden zijn ingesloten: (BmC - CnD) / 2 .

De beschreven hoek (∠AOC, Fig. 12) gevormd door twee raaklijnen (CO en AO) wordt gemeten door het halve verschil van de bogen tussen de zijden: (ABC - CDA) / 2 .

De producten van segmenten van akkoorden (AB en CD, Fig.13 of Fig.14), waarin ze worden gedeeld door het snijpunt, zijn gelijk aan: AO · BO = CO · DO.

Het kwadraat van de tangens is gelijk aan het product van de secans en zijn buitenste deel (Fig. 12): OA 2 = OB · OD. Deze eigenschap kan worden beschouwd als een speciaal geval van Fig.14.

Akkoord(AB , Afb.15) , loodrecht op de diameter( CD) , O doormidden: AO = OB.

Rijst. 15

Interessant feit:

Gefeliciteerd met je Pi-pauze.

In wetenschappelijke termen is het getal "Pi" de verhouding van de omtrek van een cirkel tot zijn diameter. Het lijkt iets eenvoudigs, maar het prikkelt de geest van wiskundigen uit de oudheid. En blijft zich zorgen maken. In die mate dat wetenschappers - zo'n 20 jaar geleden - ermee instemden om de feestdag van dit nummer te vieren. En ze riepen de hele progressieve gemeenschap op om mee te vieren. Ze doet mee: ze eet ronde Pi-hoorns, jij-pi-vaet, zeker Pi-vo en maakt de geluiden van Pi als ze elkaar ontmoeten.

Fans zullen strijden door de tekens van het nummer "Pi" te onthouden. En ze zullen proberen het record te overtreffen van de 24-jarige Chinese student Liu Chao, die zonder fouten 68890 karakters uit het hoofd noemde. Het kostte hem 24 uur en 4 minuten.

Het vertrek van de vieringen is gepland op 14 maart - een datum die in Amerikaanse spelling op 3.14 lijkt - dat wil zeggen de eerste drie cijfers van het getal "Pi".
Volgens de legende wisten de Babylonische priesters van het getal "Pi". Gebruikt bij de bouw van de toren van Babel. Maar ze konden de waarde ervan niet nauwkeurig berekenen en dit kon het project niet aan. Het symbool voor het getal "Pi" zelf werd voor het eerst gebruikt in zijn geschriften in 1706 door de wiskundige William John (William Jones). Maar in werkelijkheid schoot hij wortel na 1737 dankzij de inspanningen van de Zweedse wiskundige Leonhard Euler (Leonhard Euler).

Het vieren van de vakantie is uitgevonden door de Amerikaanse natuurkundige Larry Shaw.
Er is geen exact antwoord op de vraag hoeveel cijfers er in het getal "Pi" achter de komma staan. Hoogstwaarschijnlijk zijn het er oneindig veel. En het belangrijkste kenmerk is dat de volgorde van deze tekens niet wordt herhaald. Vandaag zijn ze bekend 12411 biljoen. 500 miljard onderzocht. En er werden geen herhalingen gevonden.

Volgens enkele vooraanstaande natuurkundigen en wiskundigen, zoals David Bailey, Peter Borwin en Simon Plouffe (David Bailey, Peter Borewin, Simon Plouffe), kunnen ze - herhalingen - door niemand worden gevonden. Schrijf tenminste het hele universum met tekens. Ja, tenminste hoeveel Universums ... En hierin zien wetenschappers een soort verborgen mystiek. Er wordt aangenomen dat in het getal "Pi" de eindeloze oerchaos, die later harmonie werd, is gecodeerd. Of wat cryptische informatie.

Vragen:

1. Wat is de definitie van cirkel en cirkel?
2. Welke nieuwe concepten ken je?
3. Wat is de plaats van punten?
4. Wat is het verschil tussen diameter en straal?
5. Hoe vind je de straal van een cirkel die wordt beschreven door een driehoek?

Lijst met gebruikte bronnen:

1. Les over het onderwerp "Visuele geometrie"
2. Savin AP De methode van geometrische plaatsen / Keuzevak in de wiskunde: leerboek voor de klassen 7-9 van de middelbare school. Samenstelling I.L. Nikolskaja. – M.: Verlichting, p. 74.
3. Smirnova I.M., Smirnov V.A. Meetkunde: een leerboek voor de rangen 7-9 van onderwijsinstellingen. – M.: Mnemosyne, 2005, p. 84.
4. Sharygin IF Geometrie. Grades 7-9: Leerboek voor algemene onderwijsinstellingen. – M.: Trap, p. 76.
5. Mazur K. I. "Het oplossen van de belangrijkste concurrentieproblemen in de wiskunde van de collectie onder redactie van M. I. Scanavi"

Aan de les gewerkt:

Samylina MV

Poturnak SA

Vladimir LAGOVSKI

U kunt een vraag stellen over modern onderwijs, een idee uiten of een urgent probleem oplossen op: Onderwijsforum waar een educatieve raad van nieuw denken en handelen internationaal bijeenkomt. hebben gemaakt blog, Je verbetert niet alleen je status als competente leraar, maar levert ook een belangrijke bijdrage aan de ontwikkeling van de school van de toekomst. Onderwijs Leiders Gilde opent de deur naar topspecialisten en nodigt je uit om mee te werken aan het creëren van de beste scholen ter wereld.

De meetkundige plaats van punten op een vlak is een figuur die bestaat uit alle punten van het vlak die een bepaalde eigenschap hebben.

T.1.29. De meetkundige plaats van punten op gelijke afstand van twee gegeven punten is de middelloodlijn op het segment dat deze punten verbindt.

In figuur 71 is de mediaan loodrecht SS op het segment getekend. T.1.29 stelt dat: a) elk punt van de lijn op gelijke afstand van A en B ligt; b) elk punt van het vlak, op gelijke afstand van A en B, ligt op een rechte lijn

Hieronder vindt u een aantal punten in het vlak.

1. De verzameling punten op een bepaalde afstand van een bepaald punt is een cirkel met het middelpunt op dat punt en met een straal gelijk aan de gegeven afstand.

2. De verzameling punten op een bepaalde afstand van een bepaalde rechte lijn bestaat uit twee rechte lijnen, die elk evenwijdig zijn aan de gegeven en zich op een bepaalde afstand daarvan bevinden.

3. De verzameling punten op gelijke afstand van twee snijdende lijnen bestaat uit twee lijnen waarop de bissectrices liggen van alle hoeken verkregen op het snijpunt van deze lijnen.

4. De verzameling punten van waaruit het lijnstuk onder een bepaalde hoek a zichtbaar is en die aan één kant van de rechte A B liggen, is een cirkelboog met uiteinden in de punten A en B.

De methode van geometrische plaatsen die wordt gebruikt bij het oplossen van constructieproblemen is gebaseerd op het volgende.

Stel dat we een punt X moeten construeren dat aan twee voorwaarden voldoet. De verzameling punten die aan de eerste voorwaarde voldoen is een figuur; de verzameling punten die aan de tweede voorwaarde voldoen is een cijfer. Het gewenste punt X behoort, d.w.z. is hun gemeenschappelijk punt.

Voorbeeld 1. Bouw langs de omtrek , hoek B gelijk aan , en hoogte , verlaagd vanaf hoekpunt A.

Oplossing. Laat het probleem worden opgelost en geconstrueerd (Fig. 72). Als we het op een rechte lijn zetten, krijgen we gelijkbenige driehoeken

Op basis van bovenstaande redenering kan de constructie in de volgende volgorde worden uitgevoerd:

1) Teken een rechte lijn en teken er een segment op

2) Trek op afstand van de rechte lijn een rechte lijn evenwijdig

3) Met het hoekpunt op punt D bouwen we een hoek gelijk aan Punt

A is een van de hoekpunten van de gewenste driehoek.

4) We tekenen de middenloodlijnen naar de segmenten Punten B en C van het snijpunt van deze middenloodlijnen met een rechte lijn - twee andere hoekpunten van de gewenste driehoek.

Het bewijs dat de gewenste wordt geleverd als volgt: de hoogte van deze driehoek is gelijk van constructie, gelijkbenig, - de buitenhoek van deze driehoek, zie T. 1. 22), van constructie.

Bijschriften van dia's:

Lesonderwerp:
"Geometrische puntenverzameling." Leraar Gordeeva N.M.
Vertel het me en ik zal het vergeten. Laat het me zien en ik zal het onthouden. Betrek me erbij en ik zal het begrijpen. (Oude Chinese wijsheid)
Het doel van de les:
kennis over het onderwerp "Methode van coördinaten" systematiseren en verdiepen.
"Een grote wetenschappelijke ontdekking biedt een oplossing voor een groot probleem, maar in de oplossing van elk probleem zit een greintje ontdekking." (Györgye Poya)
Taak:
vind de meetkundige plaats van punten die een bepaalde eigenschap hebben (een ontdekking doen).
Definitie:
De puntenverzameling is een figuur die bestaat uit alle punten in een vlak die een bepaalde eigenschap hebben.
plaats van punten,
op gelijke afstand van dit punt, zijn er
cirkel.
plaats van punten,
op gelijke afstand van de uiteinden van dit segment, zijn er
de middelloodlijn van dit segment.
plaats van punten,
op gelijke afstand van de zijden van een bepaalde hoek, zijn er
bissectrice van deze hoek.
plaats van punten,
gelijke afstand van twee evenwijdige lijnen
een rechte lijn evenwijdig aan hen die door het midden van hun gemeenschappelijke loodlijn gaat (de middelpunten van cirkels die de gegeven lijnen raken, liggen erop).
plaats van punten,
die de hoekpunten zijn van rechthoekige driehoeken met een gegeven schuine zijde, zijn
een cirkel gebouwd op de hypotenusa als diameter (exclusief de uiteinden van de hypotenusa).
plaats van punten,
de verhouding van de afstanden waarvan tot twee gegeven punten een constante waarde is, is
cirkel
(die de omtrek van Apollonius wordt genoemd).
Oefening 1
In de figuur AD=DB=2 cm. b) meer dan 2 cm; c) niet meer dan 2 cm.
een
B
EEN
D
B
Oplossing:

EEN
D
B
een
B
EEN
D
B
een
B
EEN
D
B
een
B
Taak 2
Bepaal met behulp van dezelfde figuur wat de meetkundige plaats is van punten in het vlak die zich op een afstand van punt D bevinden op een afstand gelijk aan 2 cm; b) meer dan 2 cm; c) niet meer dan 2 cm.
EEN
D
B
een
B
Oplossing:
a) De afstand van D is 2 cm:
EEN
D
B
een
B
Oplossing:
b) Afstand van D meer dan 2 cm:
EEN
D
B
een
B
Oplossing:
c) Afstand van D niet meer dan 2 cm:
EEN
D
B
een
B
Taak 3
Zoek met behulp van de coördinatenmethode een paar getallen die aan de voorwaarde voldoen
Taak 4
Bewijs met behulp van de coördinatenmethode dat het stelsel vergelijkingen een unieke oplossing heeft:
Taak 5
Bepaal GMT die voldoet aan de vergelijking: a)
Taak 5
Bepaal GMT die voldoet aan de vergelijking: b)
Taak 5
Bepaal GMT die voldoet aan de vergelijking: c)
Taak 5
Bepaal GMT die voldoet aan de vergelijking: d)
Taak 5
Bepaal GMT die voldoet aan de vergelijking: e)
Parabool als een plaats van punten.
Een parabool is de verzameling punten op gelijke afstand van een bepaald punt en van een bepaalde lijn.
Constructie van een parabool.
Hoe een bloembed te breken?
plaats van punten,
de som van de afstanden waarvan tot twee gegeven punten F1, F2 een constante waarde is; groter dan F1F2.
GMT bouwplan.
Bevestig de uiteinden van de draad met knopen aan de punten F1 en F2. Rek de draad uit met een potlood zodat de punt het papier raakt. We verplaatsen het potlood op het papier zodat de draad strak blijft staan. Trek een lijn met een potlood.
Bouw van GMT
Wat gebeurt er met de ellips als de brandpunten: a) elkaar naderen; b) uit elkaar gaan.
Vind de meetkundige plaats waarvoor de som van de afstanden tot twee gegeven punten F1 en F2: a) kleiner is dan de gegeven waarde 2a; b) meer dan de opgegeven waarde 2a.
GMT vergelijking
Bepaal de GMT die voldoet aan de vergelijking:
GMT vergelijking
, dan
- ellipsvergelijking
Antwoord: F1, F2
kegelsneden
kegelsneden
Apollonius van Perga (II-III eeuwen voor Christus) - oude Griekse wiskundige. Het belangrijkste werk - "Kegelvormige secties"
kegelsneden
Ze werden bestudeerd door oude Griekse meetkundigen. De theorie van kegelsneden was een van de hoogtepunten van de oude meetkunde.De vergelijkingen van deze lijnen werden veel later afgeleid, toen de coördinatenmethode begon te worden toegepast.
Curven van de tweede orde
ja
0
x
De methode van coördinaten in combinatie met algebra vormt een tak van meetkunde die analytische meetkunde wordt genoemd.
Ellips excentriciteit
kenmerkt de mate van verlenging.
Zelfs Johannes Kepler (1571 - 1630) - een Duitse astronoom, ontdekte dat de planeten van het zonnestelsel niet in cirkels rond de zon bewegen, zoals eerder werd gedacht, maar in ellipsen, en dat de zon zich in een van de brandpunten van deze ellipsen bevindt.
Bewegingsbanen van hemellichamen
VenusNeptunusAardePlutoDe komeet van Halley
0,0068 0,0086 0,0167 0,253 0,967
Ze hebben het probleem van een reeks punten opgelost, en deze GMT is gerelateerd aan het universum (en het was gewoon een probleem!).
Huiswerk
Stel een vergelijking op voor de meetkundige plaats, het product van de afstanden waarvan tot twee gegeven punten F1(-c; 0), F2(c; 0) een constante waarde a2 is. Zo'n locus van punten wordt het Cassini-ovaal genoemd.
Huiswerk
Stel een vergelijking op voor de meetkundige plaats, het product van de afstanden waarvan tot twee gegeven punten F1 (-a; 0), F2 (a; 0) een constante waarde a2 is. Zo'n locus van punten wordt een lemniscaat genoemd (zie figuur). (De vergelijking van de lemniscaat wordt eerst direct gevonden en wordt dan beschouwd als een bepaalde vorm van het Cassini-ovaal).
De les samenvatten

wat bezit hebben.

Voorbeelden [ | ]

Formele definitie[ | ]

In het algemeen wordt de meetkundige plaats van punten geformuleerd door het predikaat , waarvan het argument een punt van de gegeven lineaire ruimte is. Predikaatparameters kunnen van verschillende typen zijn. Het predikaat heet bepalend plaats van punten. De predikaatparameters heten differentiëlen locus van punten (niet te verwarren met het verschil in analyse).

De rol van differentiëlen bij de introductie van soortverschillen in de figuur. Het aantal verschillen kan elk zijn; Er kunnen al dan niet verschillen zijn.

Als de determinant wordt gegeven, waarbij M (\displaystyle M)- punt, - differentiëlen, dan het gewenste cijfer EEN (\displaystyle A) instellen in de vorm: EEN (\displaystyle A)- plaats van punten M (\displaystyle M), zoals dat P (M , een , b , c , ...) (\displaystyle P(M,\;a,\,b,\,c,\;\ldots))". Verder wordt meestal de rol van differentiëlen aangegeven, ze krijgen namen met betrekking tot dit specifieke cijfer. Het werkelijke cijfer wordt opgevat als een verzameling (set) van punten M (\displaystyle M), waarvoor voor elke specifieke reeks waarden a , b , c , … (\displaystyle a,\;b,\;c,\;\ldots ) stelling P (M , een , b , c , ...) (\displaystyle P(M,\;a,\,b,\,c,\;\ldots)) verandert in een identiteit. Elke specifieke set differentiële waarden definieert een afzonderlijk cijfer, die elk en allemaal in het totaal de naam van het cijfer wordt genoemd, dat wordt gespecificeerd via de GMT.

In een verbale formulering wordt een predicatieve uitspraak literair geuit, dat wil zeggen, met de betrokkenheid van verschillende soorten bochten, enz., Met het oog op eufonie. Soms, in het geval van eenvoudige determinanten, zien ze meestal af van letteraanduidingen.

Voorbeeld: we definiëren de parabool als de verzameling van al dergelijke punten M (\displaystyle M) dat de afstand van M (\displaystyle M) ter zake F (\displaystyle F) gelijk aan de afstand van M (\displaystyle M) recht doen l (\displaystyle l). Dan zijn de differentiëlen van de parabool F (\displaystyle F) en l (\displaystyle l); determinant - predikaat P (M , F , l) = (ρ (M , F) = ρ l (M , l)) (\displaystyle P(M,\;F,\;l)=(\rho (M,\;F )=\rho _(l)(M,\;l))), waar ρ (\displaystyle \rho )- afstand tussen twee punten (metrisch), ρ l (\displaystyle \rho _(l)) is de afstand van het punt tot de lijn. En ze zeggen: "Een parabool is een verzameling punten" M (\displaystyle M), op gelijke afstand van het punt F (\displaystyle F) en direct l (\displaystyle l). punt F (\displaystyle F) het brandpunt van de parabool genoemd, en de rechte lijn l (\displaystyle l)- directrice.