Lokus bodova - to je puno od svega bodovi, zadovoljavajućiodređeni navedeni uslovi.

PRIMJER 1. Srednja okomica bilo kojeg segmenta je geometrijska

mjesto bodova (tj. skup svih bodova), jednako udaljenood

krajevi ovog segmenta. Neka su PO AB i AO = OB:

Tada su udaljenosti od bilo koje točke P koja leži na srednjem okomitom PO do krajeva A i B segmenta AB jednake i jednake d.

Na ovaj način, svaka tačka medijana okomito segment ima sljedeće svojstvo: jednako je udaljen od krajeva segmenta.

Primjer 2. Simetrala kutatu jelokus tačaka jednako udaljenih od njegovih stranica.

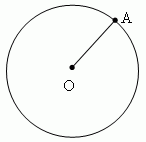
Primjer 3. Krug je mjesto tačaka (tj. Skupdržava

sve bodove), jednako udaljena od centra(slika prikazuje jedan

Iz ovih tačaka - A).

Krug - ovo je lokus tačaka (tj. skup svih točaka) na ravni,jednako udaljenaiz jedne tačke, zove središte kruga. Pozvan je segment koji povezuje središte kruga s bilo kojom od njegovih točaka radijus i označeno r ili R. Nazvan je dio ravni omeđen kružnicom okolo. Dio kruga (A m B, slika 39) luk Pozvana je ravna linija PQ koja prolazi kroz tačke M i N kruga (slika 39) secant, a njegov segment MN koji leži unutar kruga je akord.

Pozvaće se tetiva koja prolazi kroz središte kruga (na primjer, BC, slika 39) promjer i označeno d ili D. Promjer je najveća tetiva jednaka dva polumjera ( d= 2 r).

Tangenta. Pretpostavimo da sekundarni PQ (slika 40) prolazi kroz tačke K i M kruga. Pretpostavimo također da se točka M kreće duž kruga, približavajući se točki K. Tada će sekajući PQ promijeniti svoj položaj okrećući se oko točke K. Kako se točka M približi točki K, sekući PQ će težiti nekom graničnom položaju AB . Poziva se linija AB tangenta na krug u točki K. Tačka K se naziva tačka dodira. Tangensa i kružnica imaju samo jednu zajedničku tačku - tačku tangencije.

Ciljevi lekcije:

• Obrazovni: pokazati novu metodu za rješavanje problema za konstrukciju geometrijskog mjesta tačaka; Naučiti kako ga koristiti u rješavanju problema.
• Razvijanje: razvoj vizuelno-figurativnog mišljenja; kognitivni interes.
• Odgoj: razvijanje sposobnosti planiranja posla, traženje racionalnih načina izvođenja, sposobnost razumne odbrane svog mišljenja i kritička procjena rezultata.

Ciljevi lekcije:

• Učenje novog materijala.
• Testirajte sposobnost učenika za rješavanje problema.

Plan lekcije:

1. Definicije.
2. Primjer 1.
3. Primjer 2.
4. Primjer 3.
5. Teorijski dio.
6. Opšti pojmovi.

Uvod.

Drevnu egipatsku i babilonsku kulturu na polju matematike nastavili su Grci. Oni su ne samo asimilirali sva iskustva svoje geometrije, već su otišli i mnogo dalje. Naučnici drevne Grčke mogli su akumulirano geometrijsko znanje povezati u sistem i tako postaviti temelje geometrije kao deduktivne nauke.

Grčki trgovci su se upoznali s istočnom matematikom krčeći trgovačke puteve. Ali ljudi s Istoka malo su se bavili proučavanjem teorije, a Grci su to brzo otkrili. Postavljali su pitanja: zašto su u jednakokrakom trokutu dva ugla u osnovi jednaka; zašto je površina trokuta jednaka polovici površine pravougaonika sa istim osnovama i visinama?

Nažalost, nisu preživjeli primarni izvori koji opisuju rani razvoj grčke matematike. Samo zahvaljujući obnovljenim tekstovima iz četvrtog veka pre nove ere i delima arapskih naučnika, koji su bili bogati prevodima spisa autora drevne Grčke, imamo izdanja Euklida, Arhimeda, Apolonija i drugih velikih ljudi. Ali u ovim radovima je već predstavljena potpuno razvijena matematička nauka.

Drevna grčka matematika prošla je dug i težak razvojni put, počev od 6. vijeka pne. i do 6. veka. Istoričari nauke razlikuju tri perioda njenog razvoja u skladu s prirodom znanja:

1. Akumulacija odabranih matematičkih činjenica i problema (6 - 5B.B. p.n.e.).
2. Sistematizacija stečenog znanja (4 - 3 veka pre nove ere).
3. Period računske matematike (3. vek pne - 6. vek).

Težište bodova (GMT).

Definicije.

Geometrijsko mjesto- pojam koji se koristi u staroj literaturi o geometriji i koji se i danas koristi u obrazovnoj literaturi skup bodova koji zadovoljavaju određeni uslov u pravilu geometrijskog karaktera. Na primjer: žarište točaka jednako udaljenih od dviju zadanih točaka A i B je srednja točka okomita na odsječak AB. Ponekad govore o geometrijskom mjestu ravnih linija i drugim figurama.

Ime je povezano s idejom linije kao "mjesta" na kojem se nalaze točke.

U geometriji, putanja neke tačke koja se kreće u skladu sa datom formulom ili uslovom. Na primjer, krug je mjesto točke koja se kreće po ravnini tako da udaljenost od njenog mjesta do središta ostaje nepromijenjena.

Mjesto bodova (GMT) je skup točaka, koji uključuje sve točke koje zadovoljavaju određeni uvjet, i samo one.

Mjesto bodova (GMT)- figura govora u matematici, koja se koristi za definiranje geometrijske figure kao skupa točaka koje imaju neka svojstva.

Primjeri.

• Srednja točka okomita na segment je mjesto točaka jednako udaljenih od krajeva segmenta.
• Kružnica je mjesto tačaka jednako udaljenih od zadane točke, koje se naziva središte kruga.
• Parabola je mjesto tačaka jednako udaljenih od točke (koja se naziva fokus) i ravne linije (koja se naziva direktrica).

Primjer 1.

Medijan okomitog bilo kojeg segmenta je mjesto tačaka (tj. Skup svih točaka) jednako udaljenih od krajeva ovog segmenta. Neka je PO okomita na AB i AO = OB:

Tada su udaljenosti od bilo koje točke P koja leži na srednjem okomitom PO do krajeva A i B segmenta AB jednake i jednake d.

Dakle, svaka točka srednjeg okomitog na segment ima sljedeće svojstvo: jednako je udaljena od krajeva segmenta.

Primjer 2.

Simetrala kuta je mjesto tačaka jednako udaljenih od njegovih stranica.

Primjer 3.

Kružnica je žarište točaka (tj. Skup svih točaka) jednako udaljenih od svog središta (na slici je prikazana jedna od ovih točaka - A).

Akord prolazak kroz središte kruga (na primjer, BC, slika 1) naziva se promjerom i označava se d ili D. Promjer Je li najveća tetiva jednaka dva polumjera (d = 2 r).

Tangenta... Pretpostavimo da sekundarni PQ (slika 2) prolazi kroz tačke K i M kruga. Pretpostavimo također da se točka M kreće duž kruga, približavajući se točki K. Tada će sekajući PQ promijeniti svoj položaj okrećući se oko točke K. Kako se točka M približi točki K, sekundantni PQ težit će nekom graničnom položaju AB . Prava AB naziva se tangenta na kružnicu u točki K. Tačka K naziva se tačka dodira. Tangenta i kružnica imaju samo jednu zajedničku tačku - tačku tangencije.

Svojstva tangente.

1. Tangenta na kružnicu okomita je na radijus povučen na tačku dodira (AB okomita na OK, slika 2).
2. Iz točke koja leži izvan kruga možete povući dvije tangente na isti krug; njihovi su segmenti jednaki AB = AC (slika 3).

Segment Je li dio kruga omeđen lukom ACB i odgovarajućom tetivom AB (slika 4). Duljina okomitog CD-a, povučenog od sredine tetive AB do presjeka s lukom ACB, naziva se visina segmenta.

Kutovi u krugu.

Središnji ugao je kut koji čine dva polumjera (∠AOB, slika 5). Upisani ugao je kut koji čine dvije tetive AB i AC izvučene iz njihove zajedničke točke (∠BAC, slika 4). Opisani kut je kut koji čine dvije tangente AB i AC povučene iz jedne zajedničke točke (∠BAC, slika 3).

Odnosi između elemenata kruga.

Upisani ugao(∠ABC, slika 7) jednaka je polovini središnjeg ugla oslonjenog na isti luk AmC (∠AOC, slika 7). Stoga su svi upisani uglovi (slika 7) zasnovani na istom luku (AmC, slika 7) jednaki. A budući da središnji kut sadrži isti broj stepeni kao i njegov luk (AmC, slika 7), tada se svaki upisani kut mjeri polovinom luka na koji se oslanja (u našem slučaju AmC).

Svi upisani uglovi zasnovani na polukrugu (∠APB, ∠AQB,…, slika 8) su ravni.

Kut(∠AOD, slika 9), oblikovan od dva akorda (AB i CD), mjeri se poluzbrojem lukova između njegovih stranica: (AnD + CmB) / 2.

Ugao (∠AOD, slika 10) koji čine dva sekanta (AO i OD) mjeri se polovičnom razlikom luka između njegovih stranica: (AnD - BmC) / 2.

Ugao (∠DCB, slika 11) koji tvore tangenta i tetiva (AB i CD) mjeri se polovinom luka koji je u njemu zatvoren: CmD / 2.

Ugao (∠BOC, slika 12) koji tvore tangenta i sekanta (CO i BO) mjeri se polovičnom razlikom luka između njegovih stranica: (BmC - CnD) / 2.

Opisani kut (∠AOC, slika 12), koji čine dvije tangente (CO i AO), mjeri se polovičnom razlikom luka zatvorenih između njegovih stranica: (ABC - CDA) / 2.

Produkti segmenata tetiva (AB i CD, slika 13 ili slika 14), na koje su podijeljeni presječnom tačkom, jednaki su: AO · BO = CO · DO.

Kvadrat tangente jednak je umnošku sekante i njenog vanjskog dijela (slika 12): OA 2 = OB · OD. Ovo svojstvo može se smatrati posebnim slučajem sa slike 14.

Akord(AB , slika 15) okomito na promjer( CD) , O na pola: AO = OB.

Sl. petnaest

Zanimljiva činjenica:

Čestitam na P-Razdniku.

Znanstveno govoreći, pi je omjer opsega kruga i njegovog promjera. Čini se da je to jednostavna stvar, ali zabrinjava umove matematičara od davnina. I to i dalje uzbuđuje. U tolikoj mjeri da su se naučnici - prije 20 godina - složili da praznik slave na taj datum. I pozvali su čitavu naprednu zajednicu da se pridruži proslavi. Ona se pridružuje: jede okrugle Pi-roge, you-PI-vayet, nužno Pi-vo i daje zvukove Pi-a kad se sretnu.

Navijači će se natjecati sjećajući se znakova pi. Pokušat će nadmašiti rekord 24-godišnjeg kineskog studenta Liu Chaoa, koji je bez grešaka iz memorije imenovao 68890 znakova. Trebalo mu je 24 sata i 4 minute.

Odlazak s proslave zakazan je za 14. mart - datum koji u američkom pravopisu izgleda kao 3,14 - odnosno prve tri znamenke broja "Pi".
Prema legendi, babilonski svećenici znali su za broj "Pi". Koristi se za izgradnju Vavilonske kule. Ali nismo mogli precizno izračunati njegovu vrijednost i iz toga se nismo snašli u projektu. Sam simbol broja "Pi" prvi je put upotrijebio u svojim spisima 1706. godine matematičar William John (William Jones). Ali u stvarnosti je zaživio nakon 1737. godine zahvaljujući naporima švedskog matematičara Leonharda Eulera.

Američki fizičar Larry Shaw došao je na ideju da proslavi praznik.
Ne postoji tačan odgovor na pitanje koliko je cifara u broju "Pi" nakon zareza. Najvjerovatnije ih je beskonačan broj. A glavna karakteristika je da se redoslijed ovih znakova ne ponavlja. Danas je poznato 12.411 bilijuna. Istraženo 500 milijardi. I nisu pronađena ponavljanja.

Prema nekim istaknutim fizičarima i matematičarima, poput Davida Baileya, Petera Borwina i Simona Plouffea (David Bailey, Peter Borewin, Simon Plouffe), njih - ponavljanja - niko nikada neće pronaći. Barem cijeli Univerzum napišite znakovima. Da, barem koliko svemira ... I u tome naučnici vide neku vrstu skrivene mistike. Smatra se da broj "Pi" kodira beskrajni iskonski haos, koji je kasnije postao harmonija. Ili neke tajne informacije.

Pitanja:

1. Koja je definicija kruga i kruga?
2. Koje ste nove koncepte upoznali?
3. Što se naziva žarištem bodova?
4. Koja je razlika između promjera i radijusa?
5. Kako pronaći radijus kruga koji je opisan oko trokuta?

Lista korišćenih izvora:

1. Lekcija na temu "Vizualna geometrija"
2. Savin A.P. Metoda geometrijskih mjesta / Izborni predmet iz matematike: Udžbenik za 7-9 razred srednje škole. Sastavio: I.L. Nikolskaya. - M.: Obrazovanje, str. 74.
3. Smirnova I.M., Smirnov V.A. Geometrija: Udžbenik za 7-9 razred obrazovnih institucija. - M.: Mnemosina, 2005., str. 84.
4. Sharygin I.F. Geometrija. Razredi 7-9: Udžbenik za opšteobrazovne institucije. - M.: Drofa, str. 76.
5. K. Mazur "Rješenje glavnih takmičarskih zadataka iz matematike zbirke koju je uredio M. I. Skanavi"

Radili na lekciji:

Samylina M.V.

S.A.Poturnak

Vladimir LAGOVSKY

Možete postaviti pitanje o modernom obrazovanju, izraziti ideju ili riješiti hitan problem na Obrazovni forum gdje se međunarodno okuplja obrazovno vijeće svježeg razmišljanja i djelovanja. Stvaranjem blog, Ne samo da ćete povećati svoj status kompetentnog nastavnika, već ćete i značajno doprinijeti razvoju škole u budućnosti. Ceh obrazovnih vođa otvara vrata za najbolje rangirane stručnjake i poziva na saradnju u pravcu stvaranja najboljih škola na svijetu.

Lokus tačaka na ravni je lik koji se sastoji od svih točaka na ravni koje imaju određeno svojstvo.

T.1.29. Težište točaka jednako udaljenih od dviju zadanih točaka je sredina okomita na segment linije koji povezuje ove točke.

Na slici 71, srednji okomiti CC nacrtan je na segment. T.1.29 navodi da: a) je svaka točka prave linije jednako udaljena od A i B; b) svaka točka ravni koja je jednako udaljena od A i B leži na pravoj liniji

Ispod je navedeno nekoliko geometrijskih položaja tačaka u ravni.

1. Mjesto tačaka smještenih na određenoj udaljenosti od zadane točke je kružnica sa središtem u ovoj točki i polumjerom jednakim datoj udaljenosti.

2. Težište tačaka smještenih na određenoj udaljenosti od zadane prave sastoji se od dvije ravne crte, od kojih je svaka paralelna datoj i nalazi se na određenoj udaljenosti od nje.

3. Mjesto tačaka jednako udaljenih od dviju ravnih crta koje se sijeku sastoje se od dvije ravne crte na kojima leže simetrale svih uglova dobivenih na sjecištu tih ravnih linija.

4. Težište točaka iz kojih je segment vidljiv pod određenim kutom a i koje leže s jedne strane linije A B je kružni luk s krajevima u točkama A i B.

Metoda geometrijskih mjesta koja se koristi u rješavanju građevinskih problema temelji se na sljedećem.

Pretpostavimo da trebamo konstruirati točku X koja zadovoljava dva uvjeta. Lokus bodova koji zadovoljavaju prvi uvjet je slika, mjesto je bodova koji zadovoljavaju drugi uvjet, postoji lik Traženoj točki X pripada, odnosno, njihova je zajednička točka.

Primjer 1. Konstruirajte duž perimetra, ugao B jednak i visinu spuštenu sa vrha A.

Odluka. Neka se problem riješi i izgradi (slika 72). Stavljajući segmente na ravnu liniju, dobivamo jednakokrake trokute

Na osnovu gornjeg obrazloženja, gradnja se može izvesti u slijedećem slijedu:

1) Crtamo ravnu crtu i na nju položimo segment

2) Na udaljenosti od prave linije, povucite pravu liniju paralelno

3) Vrhom u tački D gradimo kut jednak Točki

A - jedan od vrhova željenog trokuta.

4) Srednje okomite crtamo na segmente tačaka B i C presjeka ovih srednjih okomitih pravaca - druga dva vrha željenog trokuta.

Dokaz da se željeni provodi na sljedeći način: visina ovog trokuta jednaka je konstrukcijom, jednakokraka, - vanjski kut ovog trokuta, vidi T. 1. 22), konstrukcijom.

Dijapozitivi:

Tema lekcije:
„Geometrijsko mjesto bodova.“ Razred 9 Učiteljica Gordeeva N.M.
Reci mi - i zaboravit ću, pokaži mi - i sjetit ću se, uključiti me - i razumjet ću. (Drevna kineska mudrost)
Svrha lekcije:
sistematizirati i produbiti znanje o temi "Metoda koordinata".
"Veliko naučno otkriće nudi rješenje velikog problema, ali u rješenju bilo kojeg problema postoji i zrno otkrića." (Gyorgye Poya)
Zadatak:
pronaći mjesto tačaka koje imaju određeno svojstvo (napraviti otkriće).
Definicija:
Lokus tačaka je lik koji se sastoji od svih točaka na ravni koje imaju određeno svojstvo.
Težište tačaka,
postoji jednako udaljena od ove tačke
krug.
Težište tačaka,
postoje jednako udaljeni od krajeva datog segmenta
sredina okomita na ovaj segment.
Težište tačaka,
postoji jednako udaljena od stranica zadanog ugla
simetrala ovog ugla.
Težište tačaka,
postoji jednako udaljena od dvije paralelne ravne linije
ravna linija paralelna s njima, koja prolazi kroz sredinu njihovog zajedničkog okomica (na njoj leže centri kružnih dodira s tim linijama).
Težište tačaka,
koji su vrhovi pravokutnih trokuta s danom hipotenuzom, postoji
krug izvučen iz hipotenuze kao promjer (isključujući krajeve hipotenuze).
Težište tačaka,
odnos udaljenosti sa kojih su dvije date točke konstantna vrijednost, je
krug
(koji se naziva Apolonijev krug).
Vježba 1
Na slici AD = DB = 2 pogledajte Koliki je lokus tačaka koje pripadaju ovoj pravoj liniji, a koje se uklanjaju iz tačke D na udaljenosti: a) jednako 2cm; b) više od 2 cm; c) ne više od 2 cm.
a
b
A
D
B
Odluka:

A
D
B
a
b
A
D
B
a
b
A
D
B
a
b
Zadatak 2
Pomoću iste slike odredite koliki je lokus tačaka ravni koje su uklonjene iz tačke D na udaljenosti a) jednakoj 2cm; b) više od 2 cm; c) ne više od 2 cm.
A
D
B
a
b
Odluka:
a) Udaljenost od D je 2cm:
A
D
B
a
b
Odluka:
b) Udaljenost od D više od 2 cm:
A
D
B
a
b
Odluka:
c) Udaljenost od D ne više od 2 cm:
A
D
B
a
b
Zadatak 3
Koristeći metodu koordinata, pronađite par brojeva koji zadovoljavaju uvjet
Zadatak 4
Koristeći koordinatnu metodu, dokažite da sistem jednadžbi ima jedinstveno rješenje:
Zadatak 5
Odredite GMT koji zadovoljava jednadžbu: a)
Zadatak 5
Odredite GMT zadovoljavajući jednačinu: b)
Zadatak 5
Odredite GMT koji zadovoljava jednadžbu: c)
Zadatak 5
Odredite GMT zadovoljavajući jednačinu: d)
Zadatak 5
Odredite GMT koji zadovoljava jednadžbu: e)
Parabola kao mjesto bodova.
Parabola je mjesto točaka jednako udaljenih od zadate točke i od zadane prave linije.
Izgradnja parabole.
Kako napraviti cvjetnjak?
Težište tačaka,
zbroj udaljenosti sa kojih su dvije zadane točke F1, F2 konstantna vrijednost; veći od F1F2.
Plan za izgradnju GMT-a.
Pričvrstite krajeve navoja pomoću gumba na točke F1 i F2. Olovkom povucite konac tako da njegov vrh dodiruje papir. Olovku ćemo premjestiti preko papira tako da konac ostane zategnut. Olovkom nacrtajte liniju.
Izgradnja HMT-a
Šta će se dogoditi s elipsom ako se žarišta: a) približe jedni drugima; b) odmaknite se jedni od drugih.
Naći mjesto tačaka za koje je zbroj udaljenosti do dviju zadatih točaka F1 i F2: a) manji od zadane vrijednosti 2a; b) više od navedene vrijednosti 2a.
HMT jednadžba
Odredite GMT koji zadovoljava jednadžbu:
HMT jednadžba
onda
- jednačina elipse
Odgovor: F1, F2
Konusni presjeci
Konusni presjeci
Apolonije iz Perge (II-III vek p. N. E.) Bio je drevni grčki matematičar. Najvažnije djelo - "Konusni profili"
Konusni presjeci
Proučavali su ih starogrčki geometri. Teorija konusnih presjeka bila je jedan od vrhunaca drevne geometrije, a jednadžbe za ove linije izvedene su mnogo kasnije kada je primijenjena koordinatna metoda.
Krive drugog reda
g
0
x
Koordinatna metoda u kombinaciji s algebrom čini granu geometrije koja se naziva analitička geometrija.
Ekscentričnost elipse
karakteriše stupanj njegovog izduživanja.
Čak je i Johannes Kepler (1571. - 1630.), njemački astronom, otkrio da se planete Sunčevog sistema ne kreću oko Sunca u krugovima, kako se ranije mislilo, već u elipsama, a Sunce je u jednom od žarišta tih elipsa.
Orbite kretanja nebeskih tijela
VenusNeptuneEarthPlutoHalley's Comet
0,0068 0,0086 0,0167 0,253 0,967
Riješili smo problem skupa bodova, a ovaj GMT ima veze sa Univerzumom (i to je bio samo problem!).
Zadaća
Napravite jednadžbu za mjesto tačaka, a umnožak udaljenosti od kojih do dvije zadane točke F1 (-c; 0), F2 (c; 0) predstavlja konstantu a2. To mjesto tačaka naziva se Cassinijev oval.
Zadaća
Napravite jednadžbu za mjesto tačaka, a umnožak udaljenosti od kojih do dvije zadane točke F1 (-a; 0), F2 (a; 0) predstavlja konstantu a2. Takav lokus tačaka naziva se lemniscate (vidi sliku). (Jednadžba lemniškata nalazi se prvo izravno, a zatim - smatrajući je određenim oblikom Cassinijevog ovala).
Sažetak lekcije

Posjedovanje neke imovine.

Primjeri [ | ]

Formalna definicija[ | ]

Općenito, mjesto tačaka formulira predikat čiji je argument točka u danom linearnom prostoru. Parametri predikata mogu biti različitih vrsta. Predikat se zove odrednica mjesto bodova. Pozvani su parametri predikata diferencijali lokus bodova (ne treba ga miješati s diferencijalom u analizi).

Uloga diferencijala u uvođenju razlika vrsta u lik. Broj razlika može biti bilo koji; možda uopšte nema razlika.

Ako je data odrednica, gdje M (\ displaystyle M)- tačka, - razlike, a zatim potrebna cifra A (\ displaystyle A) postavljen u obliku: " A (\ displaystyle A)- mjesto bodova M (\ displaystyle M) takav da P (M, a, b, c,…) (\ displaystyle P (M, \; a, \; b, \; c, \; \ ldots))". Dalje, uloga diferencijala je obično naznačena, daju im imena u odnosu na ovu određenu figuru. Sama figura shvaća se kao skup (skup) bodova M (\ displaystyle M) za koju za svaki određeni skup vrijednosti a, b, c,… (\ displaystyle a, \; b, \; c, \; \ ldots) izgovaranje P (M, a, b, c,…) (\ displaystyle P (M, \; a, \; b, \; c, \; \ ldots)) pretvara se u identitet. Svaki određeni skup diferencijalnih vrijednosti definira zasebnu brojku, od kojih se svaka i sve one u agregatu nazivaju imenom slike, koje je specificirano putem GMT-a.

U verbalnoj formulaciji, predikativna izjava se izražava literarno, to jest uz uključivanje različitih vrsta okreta, itd., U svrhu eufonije. Ponekad se, u slučaju jednostavnih odrednica, slovnih oznaka uglavnom nema.

Primjer: parabola je definirana kao skup svih takvih točaka M (\ displaystyle M) da je udaljenost od M (\ displaystyle M) do tačke F (\ displaystyle F) je jednako udaljenosti od M (\ displaystyle M) na ravno l (\ displaystyle l)... Tada su razlike parabole - F (\ displaystyle F) i l (\ displaystyle l); odrednica - predikat P (M, F, l) = (ρ (M, F) = ρ l (M, l)) (\ displaystyle P (M, \; F, \; l) = (\ rho (M, \; F ) = \ rho _ (l) (M, \; l))) gdje ρ (\ displaystyle \ rho)- udaljenost između dvije točke (metrička), ρ l (\ displaystyle \ rho _ (l))- udaljenost od tačke do ravne linije. I kažu: "Parabola je geometrijsko mjesto točaka M (\ displaystyle M) jednako udaljeni od tačke F (\ displaystyle F) i ravno l (\ displaystyle l)... Point F (\ displaystyle F) zove fokus parabole i ravna linija l (\ displaystyle l)- ravnateljica ".