Operationen med at finde en afledt kaldes differentiering.

Som et resultat af at løse problemerne med at finde afledte for de enkleste (og ikke meget simple) funktioner ved at definere den afledede som grænsen for forholdet mellem stigningen og stigningen af ​​argumentet, en tabel med afledte og præcist definerede regler for differentiering dukkede op. De første inden for at finde derivater var Isaac Newton (1643-1727) og Gottfried Wilhelm Leibniz (1646-1716).

Derfor, i vores tid, for at finde den afledede af en funktion, er det ikke nødvendigt at beregne den ovennævnte grænse for forholdet mellem funktionens stigning og stigningen af ​​argumentet, men du skal bare bruge tabel over derivater og reglerne for differentiering. Følgende algoritme er velegnet til at finde den afledede.

For at finde den afledte, skal du bruge et udtryk under streg-tegnet adskille simple funktioner og bestemme hvilke handlinger (produkt, sum, kvotient) disse funktioner er forbundet. Yderligere findes afledte af elementære funktioner i tabellen over afledte, og formlerne for afledte af produktet, sum og kvotient findes i reglerne for differentiering. Afledt tabel og regler for differentiering er givet efter de to første eksempler.

Eksempel 1. Find den afledede af en funktion

Løsning. Ud fra reglerne for differentiering finder vi ud af, at den afledte af summen af ​​funktioner er summen af ​​de afledte funktioner, dvs.

Fra tabellen over afledte finder vi ud af, at den afledede af "x" er lig med en, og den afledede af sinus er lig med cosinus. Vi erstatter disse værdier i summen af ​​afledte og finder den afledte, der kræves af problemets tilstand:

Eksempel 2. Find den afledede af en funktion

Løsning. Vi differentierer som den afledede af summen, hvor det andet led med en konstant faktor, det kan tages uden for tegnet af den afledte:

Hvis der stadig er spørgsmål om, hvor det kommer fra, bliver de som regel tydeligere efter at have gjort sig bekendt med tabellen over derivater og de enkleste differentieringsregler. Vi skal til dem lige nu.

Afledt tabel over simple funktioner

1. Afledt af en konstant (tal). Ethvert tal (1, 2, 5, 200 ...), der er i funktionsudtrykket. Altid nul. Dette er meget vigtigt at huske, da det kræves meget ofte.
2. Afledt af den uafhængige variabel. Oftest "x". Altid lig med én. Dette er også vigtigt at huske i lang tid.
3. Afledt grad. Når du løser problemer, skal du omdanne ikke-kvadratrødder til en grad.
4. Afledt af en variabel i potensen -1
5. Afledt af kvadratroden
6. Afledt af sinus
7. Afledt af cosinus
8. Afledt af tangenten
9. Afledt af cotangensen
10. Afledt af arcsine
11. Afledt af arccosinus
12. Afledt af arctangensen
13. Afledt af lysbuen cotangens
14. Afledt af den naturlige logaritme
15. Afledt af den logaritmiske funktion
16. Afledt af eksponenten
17. Afledt af eksponentialfunktionen

Differentieringsregler

1. Afledt af summen eller forskellen
2. Afledt af værket
2a. Afledt af et udtryk ganget med en konstant faktor
3. Afledt af kvotienten
4. Afledt af en kompleks funktion

Regel 1.Hvis funktioner

differentierbar på et tidspunkt, derefter på samme tidspunkt funktionerne

i øvrigt

de der. den afledede af den algebraiske sum af funktioner er lig med den algebraiske sum af de afledte funktioner af disse funktioner.

Følge. Hvis to differentierbare funktioner adskiller sig med et konstant led, så er deres afledte ens, dvs.

Regel 2.Hvis funktioner

differentierbart på et tidspunkt, så er deres produkt på samme tidspunkt også differentierbart

i øvrigt

de der. den afledte af produktet af to funktioner er lig med summen af ​​produkterne af hver af disse funktioner ved den afledte af den anden.

Konsekvens 1. Konstantfaktoren kan flyttes uden for den afledte fortegn:

Konsekvens 2. Den afledte af produktet af flere differentiable funktioner er lig med summen af ​​produkterne af den afledte af hver af faktorerne af alle de andre.

For eksempel for tre faktorer:

Regel 3.Hvis funktioner

differentierbar på et tidspunkt og , så på dette tidspunkt er det differentierbart og deres kvotientu/v, og

de der. den afledte af kvotienten af ​​to funktioner er lig med brøken, hvis tæller er forskellen mellem produkterne af nævneren og den afledte af tælleren og tælleren med den afledede af nævneren, og nævneren er kvadratet af den forrige tæller.

Hvor hvad man skal kigge efter på andre sider

Når man skal finde produktets afledte og kvotient i reelle problemer, er det altid nødvendigt at anvende flere differentieringsregler på én gang, så der er flere eksempler på disse afledte i artiklen"Afledt af et værk og en bestemt funktion".

Kommentar. Forveksle ikke en konstant (det vil sige et tal) som en summand og som en konstant faktor! I tilfælde af et led er dets afledte lig med nul, og i tilfælde af en konstant faktor tages det ud af fortegn for de afledte. Dette er en typisk fejl, der opstår i den indledende fase af at studere derivater, men efter at have løst flere en- eller to-komponent eksempler, begår den gennemsnitlige studerende ikke længere denne fejl.

Og hvis du, når du differentierer et værk eller en bestemt, har et udtryk u"v, hvori u- et tal, for eksempel 2 eller 5, det vil sige en konstant, så vil den afledede af dette tal være lig med nul, og derfor vil hele udtrykket være lig med nul (dette tilfælde er analyseret i eksempel 10).

En anden almindelig fejl er den mekaniske løsning af en afledt af en kompleks funktion som en afledt af en simpel funktion. Derfor afledet af en kompleks funktion en separat artikel er afsat. Men først vil vi lære at finde afledte af simple funktioner.

Undervejs kan du ikke undvære udtrykstransformationer. For at gøre dette skal du muligvis åbne selvstudierne i nye vinduer Handlinger med kræfter og rødder og Handlinger med brøker .

Hvis du leder efter løsninger på afledte brøker med potenser og rødder, altså når en funktion ser ud som , og følg derefter lektionen Afledt af summen af ​​brøker med potenser og rødder.

Hvis du har en opgave som f.eks , derefter din lektion "Afledninger af simple trigonometriske funktioner".

Trin for trin eksempler - hvordan man finder derivatet

Eksempel 3. Find den afledede af en funktion

Løsning. Vi bestemmer delene af funktionsudtrykket: hele udtrykket repræsenterer produktet, og dets faktorer er summer, i det andet af hvilke et af ledene indeholder en konstant faktor. Vi anvender reglen om produktdifferentiering: den afledte af produktet af to funktioner er lig med summen af ​​produkterne af hver af disse funktioner med den afledte af den anden:

Dernæst anvender vi reglen for differentiering af summen: den afledte af den algebraiske sum af funktioner er lig med den algebraiske sum af de afledte funktioner af disse funktioner. I vores tilfælde, i hver sum, den anden term med et minustegn. I hver sum ser vi både en uafhængig variabel, hvis afledte er lig med én, og en konstant (tal), hvis afledte er lig nul. Så "x" for os bliver til en og minus 5 - til nul. I det andet udtryk ganges "x" med 2, så vi gange to med den samme enhed som den afledte af "x". Vi får følgende værdier af derivaterne:

Vi erstatter de fundne afledte i summen af ​​produkterne og opnår den afledede af hele den funktion, der kræves af problemets tilstand:

Eksempel 4. Find den afledede af en funktion

Løsning. Vi er forpligtet til at finde den afledte af kvotienten. Vi anvender formlen til at differentiere kvotienten: den afledte af kvotienten af ​​to funktioner er lig med en brøk, hvis tæller er forskellen mellem produkterne af nævneren og den afledte af tælleren og tælleren og den afledte af nævneren, og nævneren er kvadratet på den foregående tæller. Vi får:

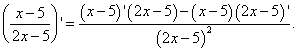
Vi har allerede fundet den afledede af faktorerne i tælleren i eksempel 2. Lad os ikke glemme, at produktet, der er den anden faktor i tælleren i det aktuelle eksempel, er taget med et minustegn:

Hvis du leder efter løsninger på problemer, hvor du skal finde den afledede af en funktion, hvor der er en kontinuerlig bunke af rødder og potenser, som f.eks. så velkommen til undervisningen "Afledt af summen af ​​brøker med potenser og rødder" .

Hvis du har brug for at lære mere om afledte af sinus, cosinus, tangenter og andre trigonometriske funktioner, altså hvornår funktionen ser ud som , så din lektion "Afledte af simple trigonometriske funktioner" .

Eksempel 5. Find den afledede af en funktion

Løsning. I denne funktion ser vi et produkt, hvor en af ​​faktorerne er kvadratroden af ​​den uafhængige variabel, hvis afledte vi har gjort os bekendt med i tabellen over afledte. I henhold til reglen om differentiering af produktet og tabelværdien af ​​den afledte af kvadratroden får vi:

Eksempel 6. Find den afledede af en funktion

Løsning. I denne funktion ser vi kvotienten, hvis udbytte er kvadratroden af ​​den uafhængige variabel. I henhold til reglen om differentiering af kvotienten, som vi gentog og anvendte i eksempel 4, og tabelværdien af ​​den afledte af kvadratroden, får vi:

For at slippe af med brøken i tælleren skal du gange tælleren og nævneren med.

Spørgsmål til eksamen på den akademiske disciplin "Elements of Higher Mathematics"

for speciale 230115 "Programmering i computersystemer"

2012 \ 2013 akademisk år.

Matricer og handlinger på dem.

(O. En nulmatrix er en matrix med alle elementer lig med 0.

O. To matricer med samme dimension mxn kaldes lige hvis i skæringspunktet mellem den i-te række og den j-te kolonne i den ene og den anden matrix er det samme nummer; i = 1, 2, ..., m; j = 1, 2, ..., n.

Lad ske EN= (a ij) er en matrix og g er et vilkårligt tal, derefter g EN= (g a ij), det vil sige, når man multiplicerer matricen A med tallet g, ganges alle de tal, der udgør matricen A, med tallet g.

Lad A og B være matricer af samme dimension A = (a ij), B = (b ij), så er deres sum A + B en matrix C = (c ij) af samme dimension, bestemt ud fra formlen c ij = a ij + b ij, det vil sige, når to matricer lægges sammen, tilføjes de tal, der er identisk placeret i dem, parvis.

Matrix A kan ganges med matrix B, det vil sige find matrix C = AB, hvis antallet af kolonner n i matrix A er lig med antallet af rækker i matrix B, mens matrix C vil have lige så mange rækker, som der er rækker i. matrix A og lige så mange kolonner som kolonner i matrix B. Hvert element i matrix C er defineret af en formel.

Elementet cij af produktmatrixen C er lig med summen af ​​produkterne af elementerne i i-rækken af ​​den første matrixfaktor med de tilsvarende elementer i den j-te kolonne i den anden matrixfaktor.

Begrebet en determinant og dens egenskaber.

Dette udtryk har andre betydninger, se. Determinant (værdier) .

Determinant(eller determinant) er et af de grundlæggende begreber lineær algebra... Determinant matricer er en polynomium fra elementerne i en kvadratisk matrix (det vil sige en, hvor antallet af rækker og kolonner er lige). Generelt matrix kan defineres over enhver kommutativ ring, i dette tilfælde vil determinanten være et element i den samme ring.

EGENSKAB 1. Værdien af ​​determinanten ændres ikke, hvis alle dens rækker erstattes af kolonner, og hver række erstattes af en kolonne med samme nummer, dvs.

EGENSKAB 2. Permutation af to kolonner eller to rækker af en determinant svarer til at gange den med -1.

EGENSKAB 3. Hvis determinanten har to identiske kolonner eller to identiske rækker, så er den lig nul.

EGENSKAB 4. Multiplikation af alle elementer i en kolonne eller en række af determinanten med et hvilket som helst tal k svarer til at gange determinanten med dette tal k.

EGENSKAB 5. Hvis alle elementer i en kolonne eller en række er lig med nul, så er selve determinanten lig nul. Denne egenskab er et særligt tilfælde af den foregående (for k = 0).

EGENSKAB 6. Hvis de tilsvarende elementer i to kolonner eller to rækker af en determinant er proportionale, så er determinanten nul.

EGENSKAB 7. Hvis hvert element i den n-te kolonne eller n-te række af determinanten er summen af ​​to led, så kan determinanten repræsenteres som summen af ​​to determinanter, hvoraf den ene i den n-te kolonne eller , henholdsvis i den n-te række har den første fra de nævnte udtryk, og den anden - den anden; elementerne på de resterende steder er de samme for milepælene for de tre determinanter.

EGENSKAB 8. Hvis vi til elementerne i en kolonne (eller en række) tilføjer de tilsvarende elementer i en anden kolonne (eller en anden række), ganget med en fælles faktor, så ændres værdien af ​​determinanten ikke. For eksempel. Yderligere egenskaber ved determinanter er relateret til begrebet et algebraisk komplement og en mol. Minor af et bestemt element er en determinant opnået fra et givet ved at slette en række og en kolonne i skæringspunktet, hvor dette element er placeret.

Det algebraiske komplement af ethvert element i determinanten er lig med minor af dette element, taget med sit eget fortegn, hvis summen af ​​tallene i rækken og kolonnen, hvor elementet er placeret, er et lige tal, og med modsat fortegn, hvis dette tal er ulige.

Vi vil betegne det algebraiske komplement af et element med et stort bogstav af samme navn og det samme tal som det bogstav, der betegner selve elementet.

EGENSKAB 9. Determinanten er lig med summen af ​​produkterne af elementer i enhver kolonne (eller række) ved deres algebraiske komplementer. Med andre ord gælder følgende ligheder:

Beregning af determinanter.

Beregningen af ​​determinanter er baseret på deres kendte egenskaber, som gælder for determinanter for alle ordener. Disse egenskaber er:

1. Hvis du omarrangerer to rækker (eller to kolonner) af determinanten, vil determinanten skifte fortegn.

2. Hvis de tilsvarende elementer i to kolonner (eller to rækker) af determinanten er lige store eller proportionale, så er determinanten nul.

3. Værdien af ​​determinanten ændres ikke, hvis du bytter rækker og kolonner, og holder deres rækkefølge.

4. Hvis alle elementer i en række (eller kolonne) har en fælles faktor, kan den tages ud af determinantens fortegn.

5. Værdien af ​​determinanten ændres ikke, hvis de tilsvarende elementer i den anden række (eller kolonne), ganget med det samme tal, lægges til elementerne i en række (eller kolonne). For determinanter af tredje orden kan denne egenskab for eksempel skrives som følger:

6. Determinanten af ​​anden orden beregnes ved formlen

7. Determinanten af ​​den tredje orden beregnes ved formlen

Der er et bekvemt skema til beregning af determinanten af ​​den tredje orden (se fig. 1 og fig. 2).

Ifølge skemaet vist i fig. 1 er produkterne af de tilsluttede elementer taget med deres eget tegn, og ifølge diagrammet i fig. 2 - med det modsatte. Værdien af ​​determinanten er lig med den algebraiske sum af de seks opnåede produkter.

Systemer af lineære ligninger. Grundlæggende begreber og definitioner.

SystemHr lineære algebraiske ligninger medn ukendt(eller, lineært system, også brugt forkortelse LANGSOM) v lineær algebra er et ligningssystem af formen

Et system af lineære ligninger i tre variable definerer et sæt fly... Skæringspunktet er løsningen.

Her er antallet af ligninger, og er antallet af ukendte. x 1 , x 2 , …, x n- ubekendte skal fastslås. -en 11 , -en 12 , …, -en mn- systemkoefficienter - og b 1 , b 2 , … b m- frie medlemmer - antages at være kendt ... Odds indekser ( -en ij) af systemet angive tallene i ligningen ( jeg) og ukendt ( j), hvor denne koefficient står hhv .

System (1) kaldes homogen hvis alle dets frie vilkår er lig med nul ( b 1 = b 2 = … = b m= 0), ellers - heterogen.

System (1) kaldes firkant hvis nummeret m ligninger er lig med tallet n ukendte.

Løsning system (1) - et sæt n tal c 1 , c 2 , …, c n sådan at substitution af hver c jeg i stedet for x jeg ind i system (1) konverterer alle sine ligninger til identiteter.

System (1) kaldes samling hvis den har mindst én løsning, og inkonsekvent hvis hun ikke har nogen løsninger.

Et fælles system af formen (1) kan have en eller flere løsninger.

Løsninger c 1 (1) , c 2 (1) , …, c n(1) og c 1 (2) , c 2 (2) , …, c n(2) et konsistent system af formen (1) kaldes forskellige hvis mindst en af ​​lighederne er overtrådt:

c 1 (1) = c 1 (2) , c 2 (1) = c 2 (2) , …, c n (1) = c n (2) .

Et fælles system af formen (1) kaldes et bestemt hvis hun har en unik løsning; hvis den har mindst to forskellige løsninger, så kaldes den udefineret... Hvis der er flere ligninger end ukendte, kaldes det omdefineret .

Metoder til løsning af lineære ligningssystemer (Cramer og Gauss metode).

Gauss metode - klassisk løsningsmetode systemer af lineære algebraiske ligninger(LANGSOM). Dette er en sekventiel undtagelsesmetode variabler, når ligningssystemet ved hjælp af elementære transformationer reduceres til et ækvivalent system af trekantet form, hvorfra, sekventielt, begyndende med de sidste (efter antal) variabler, findes alle andre variabler .

Cramers metode (Cramers regel)- en måde at løse firkantet på systemer af lineære algebraiske ligninger med ikke-nul determinant hovedmatrix(desuden, for sådanne ligninger eksisterer løsningen og er unik). Opkaldt ved navn Gabriel Kramer(1704-1752), som opfandt metoden.

Vektorer. Lineære operationer på dem.

En vektor er et rettet segment. Hvis begyndelsen af ​​vektoren er ved punkt A, og enden er ved punkt B, så betegnes vektoren AB. Hvis begyndelsen og slutningen af ​​vektoren ikke er angivet, er den angivet med det lille bogstav i det latinske alfabet a, b, c,…. Gennem BA betegner en vektor rettet modsat vektoren AB. En vektor, hvis begyndelse og slutning falder sammen, kaldes nul og betegnes med ō. Dens retning er usikker.

Længden eller modulet af en vektor er afstanden mellem dens begyndelse og slutning. Indgange | AB | og | a | betegne modulerne for vektorerne AB og a.

Vektorer kaldes kollineære, hvis de er parallelle med en ret linje, og koplanære, hvis de er parallelle med samme plan.

To vektorer siges at være ens, hvis de er kollineære, i samme retning og lige lange.

Lineære operationer på vektorer omfatter:

1) multiplikation af en vektor med et tal (Produktet af en vektor a og et tal α er en vektor betegnet med α ∙ a. (Eller omvendt a ∙ α), hvis modul er | α a | = | α || a |, og retningen falder sammen med retningen af ​​vektoren a hvis α> 0, og modsat den hvis α< 0.

2) addition af vektorer (Summen af ​​vektorer er en vektor, angivet med begyndelsen af ​​hvis begyndelse er i begyndelsen af ​​den første vektor en 1, og slutningen - i slutningen af ​​den sidste vektor an, en stiplet linje bestående af en sekvens af vektorled. Denne additionsregel kaldes reglen om at lukke en stiplet linje. summen af ​​to vektorer, det svarer til parallelogramreglen)

Den rette linje e med retningen angivet på den, taget som positiv, kaldes e-aksen.

En lineær kombination af vektorer a i er en vektor a bestemt af formlen, hvor er nogle tal.

Hvis for et system med n vektorer a i ligheden

er kun sandt, hvis dette system kaldes lineært uafhængigt. Hvis lighed (1) gælder for mindst én af dem er ikke-nul, så kaldes systemet af vektorer aі lineært afhængigt. For eksempel er alle kollineære vektorer, tre koplanære vektorer, fire eller flere vektorer i tredimensionelt rum altid lineært afhængige.

Tre ordnede lineært uafhængige vektorer ē 1, ē 2, ē 3 i rummet kaldes en basis. En ordnet triplet af ikke-koplanære vektorer danner altid en basis. Enhver vektor a i rummet kan udvides i basis ē 1, ē 2, ē 3, dvs. a kan repræsenteres som en lineær kombination af basisvektorer: a = xē 1 + yē 2 + zē 3, hvor x, y, z er koordinatvektor a i basis ē 1, ē 2, ē 3. En basis kaldes ortonormal, hvis dens vektorer er indbyrdes vinkelrette og har enhedslængde. Et sådant grundlag er betegnet med i, j, k, dvs. i = (1,0,0), j = (0, 1, 0), k = (0, 0, 1).

Eksempel 5. Vektorer er specificeret i en ortonormal basis i, j, k ved koordinater: a = (2; -1; 8), е 1 = (1,2,3), е 2 = (1, -1, - 2), e3 = (1, -6,0). Sørg for, at triplen e 1, e 2, e 3 danner en basis, og find vektorens koordinater i denne basis.

Løsning. Hvis determinanten , sammensat af koordinaterne for vektorerne e 1, e 2, e 3, ikke er lig med 0, så er vektorerne e 1, e 2, e 3 lineært uafhængige og danner derfor en basis. Vi sikrer os, at = -18-4 + 3-12 = -31 Således er det tredobbelte e 1, e 2, e 3 et grundlag.

Lad os betegne koordinaterne for vektoren a i basis е 1, е 2, е 3 ved x, y, z. Så er a = (x, y, z) = хе 1 + yе 2 + zе 3. Da ved betingelsen a = 2i - j + 8k, e 1 = i + 2j + 3k, e 2 = i - j -2k, e 3 = i - 6j, så fra ligheden a = xe1 + ye 2 + ze 3 det følger sådan, at 2i - j + 8k = xi + 2xj + 3xk + yi - yj -2yk + zi -6zj = (x + y + z) i + (2x-y-6z) j + (3x-2y) k .. Som du kan se, er vektoren på venstre side af den resulterende lighed lig med vektoren på højre side, og dette er kun muligt, hvis deres tilsvarende koordinater er ens. Derfor får vi et system til at finde de ukendte x, y, z:

Dens løsning: x = 2, y = -1, z = 1. Så a = 2e 1 - e 2 + e 3 = (2, -1,1).

Nedbrydning af vektorer. Punktprodukt af vektorer.

Skalært produkt Sommetider indre arbejde- operation på to vektorer, hvis resultat er tallet ( skalar), som ikke afhænger af koordinatsystemet og karakteriserer længderne af faktorvektorerne og vinklen mellem dem. Denne operation svarer til multiplikation længde vektor x på projektion vektor y med vektor x. Denne operation ses normalt som kommutativ og lineær for hver faktor.

En af følgende konventioner er almindeligt anvendt:

eller ( betegnelse Dirac ofte brugt i kvantemekanik for tilstandsvektorer):

Normalt antages det, at prikproduktet er positivt bestemt, dvs

For alle .

Hvis dette ikke er forudsat, så kaldes arbejdet ubestemt.

Prik produkt v vektor rum over Mark kompleks(eller materiale) tal kaldes en funktion for elementer, der tager værdier i (eller), defineret for hvert par af elementer og opfylder følgende betingelser:

Bemærk, at det følger af definitionens punkt 2. Derfor giver punkt 3 mening på trods af de komplekse (i det generelle tilfælde) værdier prik produkt.

Vektorprodukt af vektorer.

Vektor produkt- dette er pseudovektor, vinkelret plan konstrueret ud fra to faktorer, hvilket er resultatet binær operation"Vektor multiplikation" over vektorer i tredimensional Euklidisk rum... Arbejdet er hverken det ene eller det andet kommutativ heller ikke associativ(det er antikommutativ) og adskiller sig fra prikprodukt af vektorer... I mange ingeniør- og fysikproblemer er det nødvendigt at kunne konstruere en vektor vinkelret på de to eksisterende – krydsproduktet giver denne mulighed. Krydsprodukt er nyttigt til at "måle" vinkelret på vektorer - længden af ​​krydsproduktet af to vektorer er lig med produktet af deres længder, hvis de er vinkelrette, og falder til nul, hvis vektorerne er parallelle eller antiparallelle.

Krydsproduktet kan defineres på forskellige måder, og teoretisk, i et rum af enhver dimension n du kan beregne produktet n-1 vektorer, hvorved der opnås en enkelt vektor vinkelret på dem alle. Men hvis produktet er begrænset til ikke-trivielle binære produkter med vektorresultater, så er det traditionelle vektorprodukt kun defineret i tredimensionelle og syv-dimensionelle mellemrum. Resultatet af et vektorprodukt afhænger ligesom et skalarprodukt af målinger Euklidisk rum.

I modsætning til formlen til beregning af vektorernes koordinater prik produkt i tredimensional rektangulært koordinatsystem, formlen for krydsproduktet afhænger af orientering rektangulært koordinatsystem eller med andre ord dets " chiralitet».

Blandet produkt af vektorer

Blandet arbejde vektorer - skalært produkt vektor på krydsprodukt vektorer og :

Det kaldes nogle gange triple dot produkt vektorer, højst sandsynligt på grund af det faktum, at resultatet er skalar(mere præcist - pseudoskalær).

Geometrisk betydning: Modulet af det blandede produkt er numerisk lig med volumenet parallelepipedum dannet af vektorer .

Blandet arbejde skæv-symmetrisk i forhold til alle dens argumenter:

det vil sige, at en permutation af to vilkårlige faktorer ændrer produktets fortegn. Derfor følger det

I særdeleshed,

Et blandet værk er bekvemt skrevet vha symbol (tensor) Levi-Civita:

(i den sidste formel i den ortonormale basis kan alle indekser skrives med lavere; i dette tilfælde gentager denne formel fuldstændigt formlen med determinanten, men i dette tilfælde faktoren (-1) for de venstre baser opnås automatisk).

Kartesisk rektangulært koordinatsystem på et plan.

Tag på flyet to indbyrdes vinkelrette rette linjer - to koordinatakser Ox og Oy med positive retninger angivet på dem (fig. 1). Lige linjer Ox og Oy kaldes koordinatakser, punktet for deres skæringspunkt O - oprindelsen.

Koordinatakser Ox, Oy med den valgte skalaenhed kaldes et kartesisk rektangulært (eller rektangulært) koordinatsystem på planet.

Til et vilkårligt punkt M i flyet sætter vi to tal i korrespondance: abscissen x, lig med afstanden fra punkt M til aksen Oy, taget med et "+"-tegn, hvis M er til højre for Oy, og med et "-"-tegn, hvis M er til venstre for Oy; ordinaten y, lig med afstanden fra punktet M til Ox-aksen, taget med et "+"-tegn, hvis M ligger over Ox, og med et "-"-tegn, hvis M er under Ox. Abscissen x og ordinaten y kaldes de kartesiske rektangulære koordinater for punktet M (x; y).

Oprindelsen har koordinater (0; 0). Koordinatakserne deler planet i fire dele kaldet kvarte eller kvadranter (nogle gange også kaldet koordinatvinkler). Den del af planet, der er indesluttet mellem de positive halvakser Oх og Oy, kaldes den første kvadrant. Yderligere går nummereringen af ​​kvadranterne mod uret (fig. 2). For alle punkter i I-kvadranten x> 0, y> 0; for punkt I I i kvadrant x<0, у>0, i I I I-kvadranten x<0, у<0 и в IV квадранте х>0, y<0.

Polære koordinater.

Polar koordinatsystem- et todimensionalt koordinatsystem, hvor hvert punkt på et plan er defineret af to tal - en polær vinkel og en polær radius. Det polære koordinatsystem er især nyttigt, når forhold mellem punkter er nemmere at repræsentere med hensyn til radier og vinkler; i de mere almindelige, kartesisk eller et rektangulært koordinatsystem, kan sådanne relationer kun etableres ved at anvende trigonometrisk ligninger.

Det polære koordinatsystem er defineret af en stråle, som kaldes nul- eller polaksen. Det punkt, hvorfra denne stråle kommer ud, kaldes oprindelsen eller polen. Ethvert punkt på et plan er defineret af to polære koordinater: radial og vinkel. Den radiale koordinat (normalt betegnet) svarer til afstanden fra punktet til origo. Vinkelkoordinat, også kaldet polarvinkel el azimuth og er angivet lig med den vinkel, som polaksen skal drejes mod uret med for at komme til dette punkt.

Den radiale koordinat bestemt på denne måde kan tage værdier fra kradse Før uendelighed, og vinkelkoordinaten går fra 0 ° til 360 °. Men for nemheds skyld kan rækkevidden af ​​værdier for den polære koordinat udvides ud over grænsen

Ligning for en ret linje på et plan

Definition. Enhver ret linje på et plan kan gives ved en førsteordens ligning

Axe + Wu + C = 0,

og konstanterne A, B er ikke lig med nul på samme tid. Denne førsteordens ligning kaldes den generelle ligning for den rette linje. Afhængigt af værdierne af konstanterne A, B og C er følgende specielle tilfælde mulige:

C = 0, A ≠ 0, B ≠ 0 - linjen går gennem origo

A = 0, B ≠ 0, C ≠ 0 (By + C = 0) - den rette linje er parallel med Ox-aksen

B = 0, A ≠ 0, C ≠ 0 (Ax + C = 0) - den rette linje er parallel med Oy-aksen

B = C = 0, A ≠ 0 - den rette linje falder sammen med Oy-aksen

A = C = 0, B ≠ 0 - den rette linje falder sammen med Ox-aksen

Ligningen for en ret linje kan præsenteres i forskellige former afhængigt af givne begyndelsesbetingelser.

De vigtigste problemer ved at bruge ligningen for den rette linje

Jeg kan ikke svare

Anden ordens kurver

Anden ordens kurve er stedet for punkter, hvis kartesiske rektangulære koordinater opfylder en ligning af formen

hvor mindst en af ​​koefficienterne er ikke-nul.

Nummerrækkefølgegrænse og funktioner

Grænse for en numerisk sekvens. Overvej en numerisk sekvens, hvis almindelige term nærmer sig et bestemt antal -en forøgelse af serienummeret n... I dette tilfælde siges talrækken at have begrænse... Dette begreb har en strengere definition.

Denne definition betyder det -en der er begrænse en numerisk sekvens, hvis dens almindelige term nærmer sig uendeligt -en med stigende n... Geometrisk betyder det, at man for enhver > 0 kan finde et sådant tal N det starter med n > N alle medlemmerne af sekvensen er placeret inden for intervallet ( -en -en). En sekvens, der har en grænse kaldes konvergerende; Ellers - divergerende.

Rækkefølgen kaldes begrænset hvis der er et sådant nummer M hvad | u n | M  for alle n . En stigende eller faldende sekvens kaldes monotont.

Grundlæggende teoremer om grænser og deres anvendelser

Sætning 1 . (om overgangen til grænsen for ligestilling) Hvis to funktioner tager de samme værdier i nærheden af ​​et punkt, så falder deres grænser på dette tidspunkt sammen.

Sætning 2. (om overgangen til grænsen i uligheden) Hvis værdierne af funktionen f(x) i et område af et punkt ikke overskride de tilsvarende værdier af funktionen g(x) , derefter grænsen for funktionen f(x) på dette tidspunkt ikke overskrider grænsen for funktionen g(x) .

Sætning 3 . Grænsen for en konstant er lig med den mest konstante.

Bevis. f(x) = med, det vil vi bevise.

Tag vilkårlig > 0. Som  kan du tage evt

positivt tal. Så kl

Sætning 4. Fungere kan ikke have to forskellige grænser i

et point.

Bevis. Antag det modsatte. Lad ske

og .

Ved sætningen om sammenhængen mellem grænsen og en infinitesimal funktion:

f(x)- EN= - b.m. kl,

f(x)- B= - b.m. kl.

Hvis vi trækker disse ligheder fra, får vi:

B-EN= - .

Når vi passerer til grænserne på begge sider af ligestillingen, har vi:

B-EN= 0, dvs. B=EN... Vi får en modsigelse, der beviser sætningen.

Sætning 5. Hvis hvert led i den algebraiske sum af funktioner har en grænse ved, så har den algebraiske sum også en grænse ved, og grænsen for den algebraiske sum er lig med den algebraiske sum af grænserne.

.

Bevis. Lad ske , , .

Så ved sætningen om sammenhængen mellem grænsen og b.m... funktioner:

hvor - b.m. kl.

Lad os tilføje disse ligheder algebraisk:

f(x)+ g(x)- h(x) - (A + B-C)= ,

hvor b.m. kl.

Ved sætningen om sammenhængen mellem grænsen og infinitesimalen funktioner:

A + B-C= .

Sætning 6. Hvis hver af faktorerne i produktet af et begrænset antal funktioner har en grænse ved, så har produktet også en grænse ved, og grænsen for produktet er lig med produktet af grænserne.

.

Følge. Den konstante multiplikator kan tages uden for grænsetegnet.

.

Sætning 7. Hvis funktioner f(x) og g(x) har en grænse ved,

desuden har deres kvotient en grænse ved, og kvotientgrænsen er lig med kvotienten af ​​grænserne.

, .

Kontinuitet i funktion

I fig. 15, og grafen for funktionen vises ... Det er naturligt at kalde det en kontinuerlig graf, fordi den kan tegnes med et blyantstrøg uden at rive af papiret. Lad os sætte et vilkårligt punkt (tal). Et andet punkt tæt på det kan skrives i den form, hvor der er et positivt eller negativt tal, kaldet en stigning. Forskel

kaldes funktionens stigning i det punkt, der svarer til stigningen. Det, der menes her, er det ... I fig. 15, og lig med længden af ​​segmentet.

Vi vil have en tendens til nul; så, for funktionen under overvejelse, er det indlysende, at den vil tendere mod nul:

. (1)

Betragt nu grafen i figur 15, b. Den består af to sammenhængende stykker og. Disse brikker er dog ikke forbundet kontinuerligt, og derfor er det naturligt at kalde grafen for diskontinuerlig. For at grafen skal afbilde en funktion med en enkelt værdi i et punkt, er vi enige om, at den er lig med længden af ​​segmentet, der forbinder og; som tegn på dette vises punktet på grafen med en cirkel, mens punktet er tegnet med en pil, der angiver, at det ikke hører til grafen. Hvis punktet tilhørte grafen, ville funktionen være tocifret i punktet.

Lad os nu tilføje en stigning og definere den tilsvarende stigning af funktionen:

Hvis vi har en tendens til nul, så kan vi nu ikke længere sige, at det vil have en tendens til nul. For negative dem, der har en tendens til nul, er dette tilfældet, men for positive er det slet ikke tilfældet: af figuren kan det ses, at hvis, mens de forbliver positive, har tendens til nul, så tenderer den tilsvarende stigning til et positivt tal, der er lig med til segmentets længde.

Efter disse overvejelser er det naturligt at kalde en funktion defineret på et segment kontinuert i et punkt af dette segment, hvis dets stigning på dette punkt svarende til stigningen har tendens til nul for enhver metode til tendens til nul. Dette (egenskaben kontinuitet i) er skrevet i form af relation (1) eller på denne måde:

Record (2) lyder således: grænsen er nul, når den har tendens til nul ifølge enhver lov. Imidlertid udelades udtrykket "ifølge enhver lov" normalt, hvilket antyder det.

Hvis en funktion defineret på ikke er kontinuert i et punkt, det vil sige, hvis egenskab (2) ikke gælder for den i det mindste for én måde at vende mod nul, så kaldes den diskontinuerlig i et punkt.

Funktionen vist i fig. 15, a, er kontinuerlig på ethvert punkt, mens funktionen vist i fig. 15b er naturligvis kontinuerlig på ethvert punkt, undtagen for punktet, fordi for sidstnævnte er relation (2) ikke opfyldt, når den forbliver positiv.

En funktion, der er kontinuert på et hvilket som helst punkt i et segment (interval), kaldes kontinuert på dette segment (interval).

En kontinuert funktion udtrykker matematisk en egenskab, som vi ofte møder i praksis, hvilket er, at et lille trin af en uafhængig variabel svarer til et lille trin af en afhængig variabel (funktion). Forskellige bevægelseslove for legemer, der udtrykker afhængigheden af ​​den vej, som kroppen gennemløber til tiden, kan tjene som fremragende eksempler på en kontinuerlig funktion. Tid og rum er kontinuerlige. En eller anden bevægelseslov etablerer mellem dem en vis kontinuerlig forbindelse, kendetegnet ved, at en lille stigning i tiden svarer til en lille stigning i stien.

En person kom til abstraktionen af ​​kontinuitet ved at observere de såkaldte kontinuerlige medier omkring ham - fast, flydende eller gasformigt, for eksempel metaller, vand, luft. Faktisk er ethvert fysisk miljø en klynge af et stort antal bevægelige partikler adskilt fra hinanden. Disse partikler og afstandene mellem dem er imidlertid så små i forhold til de medievolumener, som skal håndteres i makroskopiske fysiske fænomener, at mange sådanne fænomener kan studeres ganske godt, hvis vi antager, at massen af ​​mediet under Studiet er omtrent kontinuerligt fordelt uden huller i den plads, den optager. Mange fysiske discipliner er baseret på denne antagelse, for eksempel hydrodynamik, aerodynamik og elasticitetsteorien. Det matematiske kontinuitetsbegreb spiller naturligvis en vigtig rolle i disse discipliner, som i mange andre.

Kontinuerlige funktioner udgør hovedklassen af ​​funktioner, som matematisk analyse opererer med.

Eksempler på kontinuerte funktioner er elementære funktioner (se § 3.8 nedenfor). De er kontinuerlige med de intervaller af forandringer, hvor de er defineret.

Diskontinuerlige funktioner i matematik afspejler diskontinuerlige processer, der forekommer i naturen. Ved stød ændres værdien af ​​kroppens hastighed for eksempel brat. Mange kvalitetsovergange er ledsaget af spring. For eksempel forholdet mellem temperaturen på et gram vand (is) og antallet af kalorier af varme i det, når det skifter mellem og, hvis det er konventionelt accepteret, at for, er værdien udtrykt ved følgende formler:

Vi mener, at isens varmekapacitet er 0,5. Når denne funktion viser sig at være udefineret - multivalued; for nemheds skyld kan det aftales, at det f.eks. får en veldefineret værdi. Funktionen er åbenbart diskontinuerlig ved, er vist i fig. 16.

Lad os give en definition af kontinuiteten af ​​en funktion i et punkt.

En funktion kaldes kontinuert i et punkt, hvis den er defineret i et eller andet område af dette punkt, inklusive ved selve punktet, og hvis dens stigning på dette punkt, svarende til stigningen af ​​argumentet, har en tendens til nul som:

Hvis vi sætter, så får vi følgende ækvivalente definition af kontinuitet i: en funktion er kontinuert i et punkt, hvis den er defineret i et eller andet område af dette punkt, inklusive ved selve punktet, og hvis

; (4)

eller andet i sproget: hvis der for alle er sådan at

Ligestilling (4) kan også skrives som følger:

. (4’)

Det viser, at man under tegnet af en kontinuerlig funktion kan passere til grænsen.

EKSEMPEL 1. En konstant er en funktion, der er kontinuert på ethvert punkt. Faktisk svarer et punkt til værdien af ​​en funktion, et punkt svarer til den samme værdi ... Derfor

.

PRI me R 2. Funktionen er kontinuert for enhver værdi, fordi og derfor kl.

PRI me R 3. Funktionen er kontinuerlig for evt. Ja,

Men for enhver, uligheden

Hvis, så følger dette af fig. 17, som viser en cirkel med radius 1 (længdebuen er større end den korde, der er kontraheret af den, har en længde). For ulighed (6) bliver til lighed. Hvis så ... Til sidst, hvis, så ... Af (5) på grundlag af (6) følger

,

Men så åbenbart

Du kan også sige, at for alle kan du finde præcis sådan

Vi bemærker en vigtig sætning.

SÆTNING 1. Hvis funktioner og er kontinuerte i et punkt, så er deres sum, forskel, produkt og kvotient (at) også kontinuerte på dette punkt.

Denne sætning følger direkte af sætning 6 i §3.2, hvis vi tager højde for det i dette tilfælde

En vigtig sætning om kontinuiteten af ​​en funktion af en funktion (sammensat funktion) er også sand.

SÆTNING 2. Lad der gives en funktion, der er kontinuert i et punkt, og en anden funktion, der er kontinuert i et punkt, og lad. Så den komplekse funktion er kontinuerlig på et punkt.

Bevis. Bemærk, at ved definitionen af ​​kontinuiteten af ​​en funktion i et punkt, følger det, at den er defineret i et eller andet område af dette punkt. Derfor

Her indførte vi en substitution og tog højde for kontinuiteten på punktet .

EKSEMPEL 4. Funktion

hvor er konstante koefficienter, kaldes et gradspolynomium. Det er kontinuerligt for enhver. Når alt kommer til alt, for at få, er det nødvendigt, baseret på konstante tal og en funktion, at udføre et endeligt antal aritmetiske operationer - addition, subtraktion og multiplikation. Men en konstant er en kontinuert funktion (se eksempel 1), og funktionen er også kontinuert (se eksempel 2), så kontinuiteten følger af sætning 1.

EKSEMPEL 5. Funktionen er kontinuerlig. Det er en sammensætning af to kontinuerlige funktioner:,.

EKSEMPEL 6. Funktion

er kontinuert for de angivne, fordi den (se sætning 1) er lig med kvotienten af ​​divisionen af ​​kontinuerte funktioner og divisoren ikke er lig med nul (for de angivne).

EKSEMPEL 7. Funktion

er kontinuert for enhver, fordi det er en sammensætning af kontinuerte funktioner:,, (se sætning 2).

EKSEMPEL 8. Funktionen er kontinuerlig pga

EKSEMPEL 9. Hvis en funktion er kontinuert i et punkt, så er funktionen også kontinuert på dette punkt.

Dette følger af sætning 2 og eksempel 8, fordi en funktion er en sammensætning af to kontinuerte funktioner,.

Vi bemærker yderligere to sætninger, som direkte følger af de tilsvarende sætninger 1 og 2 i §3.2 for grænsen for en funktion.

SÆTNING 3. Hvis en funktion er kontinuert i et punkt, så er der et kvarter til dette punkt, hvorpå den er afgrænset.

SÆTNING 4. Hvis funktionen er kontinuert i punktet u, så eksisterer der et naboskab til punktet, hvor

.

Desuden, hvis, så

og hvis, så

Afledt koncept.

Afledte(fungerer på et punkt) - grundlæggende koncept differentialregning karakterisering af ændringshastigheden af ​​funktionen (på et givet punkt). Defineret som begrænse forholdet mellem funktionstilvæksten og dens tilvækst argument når man har tendens til at øge argumentet til nul hvis en sådan grænse findes. En funktion, der har en endelig afledt (på et tidspunkt) kaldes differentierbar (på et givet punkt).

Processen med at beregne den afledte kaldes differentiering... Omvendt proces - at finde antiderivat - integration.

Den geometriske og mekaniske betydning af derivatet.

Differentieringsregler.

Afledt af en algebraisk sum af funktioner

Sætning 1. Afledte summen (forskellen) af to differentierbare funktioner er lig summen (forskellen) af afledte funktioner af disse funktioner:

(u ± v) "= u" ± v "

Følge. Den afledte af en endelig algebraisk sum af differentiable funktioner er lig med den samme algebraiske sum af de afledte led. For eksempel,

(u - v + w) "= u" - v "+ w"

Den afledte af produktet af funktioner bestemmes af

Sætning 2. Den afledte af produktet af to differentierbare funktioner er lig med produktet af den første funktion ved den afledede af den anden plus produktet af den anden funktion med den afledte af den første, dvs.

(uv) "= u" v + uv "

Konsekvens 1. Konstantfaktoren kan tages uden for fortegnet for den afledte (cv) "= cv" (c = const).

Konsekvens 2. Den afledte af produktet af flere differentiable funktioner er lig med summen af ​​produkterne af den afledte af hver af dem af alle de andre.

For eksempel (uvw) "= u" vw + uv "w + uvw"

Afledt af kvotienten af ​​to funktioner

er udtrykt ved følgende sætning.

Sætning 3. Den afledte af kvotienten af ​​to differentiable funktioner er defineret af formlen

Den afledte af en kompleks funktion udtrykker

Sætning 4. Hvis y = f (u) og u = (φ (x)) er differentiable funktioner af deres argumenter, så derivat af en sammensat funktion y = f (f (x)) eksisterer og er lig med produktet af den afledede af denne funktion med hensyn til mellemargumentet med den afledede af mellemargumentet med hensyn til den uafhængige variabel, dvs.

Meget ofte i test i matematik for derivater komplekse funktioner gives, f.eks. y = sin (cos5x). Den afledte af en sådan funktion er -5sin5x * sin (cos5x)

Se et eksempel på beregning af en kompleks funktion i den følgende video.

Afledte af elementære funktioner.

Afledninger af elementære funktioner af et simpelt argument	Fungerey = f (kx + b )	Afledninger af elementære funktioner af et komplekst argument
y=xn	y=nxn−1	y=(kx+b)n	y=nk(kx+b)n−1
		y=(kx+b)

Derfor spiller lighed (3.10) en vigtig rolle både i teoretiske undersøgelser og i tilnærmede beregninger.

Operationer til at finde den afledede og differentiale af en funktion kaldes differentiering denne funktion. Det fælles navn for begge operationer skyldes deres åbenlyse afhængighed. I kraft af formlen (3.8) opnås differentialet for en funktion ved simpel multiplikation af dens produkt

relative fejl, der opstår, når stigningen af ​​en funktion erstattes af dens differentiale.

Find tilvæksten og differentialet for funktionen

y = 3 (x + x) 2 + (x + x) - 3 x2 - x = 6 x x + 3 (x) 2 + x = (6 x + 1) x + (x) 2.

Så dy = (6 x + 1) x. Beregn y og dy i punktet x = 1, hvis x = 0, 1 y = 7 0, 1 + 3 0, 01 = 0, 73; dy = 7 0, 1 = 0, 7.

Den absolutte fejl y - dy = 0, 73 - 0, 7 = 0, 03 og den relative fejl

y = 0 0,03 73 ≈0,04.

3.5. Afledt af summen, produktet og kvotienten af ​​funktioner

Lad os huske de differentieringsregler, der er kendt fra gymnasiet, som i nogle tilfælde tillader at finde afledte funktioner uden at ty direkte til definitionen.

Sætning 3.3. Hvis funktionerne u = u (x) og v = v (x)

ved punkt x, derefter på dette punkt
				(u + v)
				(uv)		U v + v u;
					u v - v u				V = v (x) ≠ 0.

differentierbar

Hvis vi multiplicerer disse lighedsled med dx, får vi de samme regler skrevet med hensyn til differentialerne

d (u + v) = du + dv;
d (uv) = udv + vdu;

					udv - vdu

Bevis. Da beviset er fuldstændig ensartet for alle dele af sætningen, beviser vi en af ​​dem, for eksempel den anden.

Vi sætter y = uv. Giv x en stigning på x, og lad

u, Δ v, Δ y vil være inkrementerne af funktionerne u, v, y i punktet									x, svarende til
stigende		x, argument. Derefter
y = (u + u) (v + v) - uv = v u + u v + u v.
I betragtning af at u	og v er værdierne af funktioner i punktet							x er ikke afhængig af
vokser et argument		x, i kraft af definition (3.1) og begrænsningens egenskaber
overgang (se formlerne (2.14), (2.15), finder vi
y ′ = lim		V lim		U lim	v + lim
x → 0		x → 0		x → 0		x → 0		x → 0
Funktion v = v (x)	på det pågældende punkt					x ved sætningens hypotese

er refererbar og derfor kontinuerlig (sætning 3.2), derfor

	v = 0 (definition af kontinuitet 2.17) og den foregående lighed
x → 0					y ′ = vu ′ + uv ′ + u 0. Erstatter her
giver et udtryk for den afledede:
y = uv, kommer vi til formlen (3.12).							y = C (her
	Afledt og differential af en konstant funktion
MED -	konstant tal for alle x X)					er lig med nul.
	x X C
					dC = C dx = 0.
Faktisk har en sådan funktion en sådan funktion på alle punkter i mængden X
og samme betydning, i kraft af hvilken for hende						y ≡ 0 for enhver	x og x sådan
	x, x + x X. Derfor,			i kraft af definitionen af ​​derivatet og
renial, formler (3.17) følger.
	Formel (3.11) er generaliseret til tilfældet med ethvert endeligt antal svage
funktioner.
	For u = C, hvor	C - const, formlerne (3.12) og (3.15),					i kraft af (3.17),
				d (Cv) = Cdv. Det vil sige en konstant multiplikator
give ligheder: (Cv)

kroppen kan tages ud for tegnene for den afledte og differentiale.

I tilfælde af tre faktorer, successivt at anvende formlen

(3.12), finder vi

(uvw) ′ = ((uv) w) ′ = (uv) ′ w + (uv) w ′ + (u ′ v + uv ′) w + uvw ′ = = u ′ vw + uv ′ w + uvw.

En lignende regel er gyldig, når man differentierer produktet af et vilkårligt antal faktorer.

I de følgende afsnit vil de afledte elementære funktioner blive opnået.

3.6. Afledte trigonometriske funktioner

Lad os finde de afledte trigonometriske funktioner, nemlig

		Cosx						= - sinx
	(synd x)					(cos x)
	(tgx) ′ =					(ctgx)"
			cos2 x						synd 2 x

Lad os få den første. Tilvæksten af ​​funktionen y = sin x i punktet x, co-

	tilsvarende stigning				argument vil være
	y = sin (x +		x) - sinx = 2sin				x cos (x +		x).
	I betragtning af at synd 2 x		2 x kl
						x → 0	og ved at bruge definitionen af
	vand, finder vi				2sin 2 x cos (x +			2x)
	y ′ = lim		y = lim
		x → 0		x → 0
		2 2 x cos (x +		2x)		Limcos (x +		x) = cosx.
	x → 0					x → 0

Den anden formel er bevist på en lignende måde. Den tredje og fjerde formel fås ved at udtrykke tangenten og cotangensen i form af sinus og cosinus og bruge formel (3.13).

3.7. Differentiering af logaritmiske funktioner

	Følgende formler er gyldige
					loga e
		(loga x)				2. (lnx)

Lad os bevise den første af dem. Forøgelsen af ​​funktionen y = log a x i punktet x, co-

svarende til stigningen x		argument vil være
y = loga (x + x) - loga x = loga		x + x	Loga (1+	x) = loga e ln (1+	x);

(vi brugte her identitetslog a A = log a e ln A).

Siden ln (1 + x x) x x		x → 0		Derefter per definition den afledte
vi får:	y = loga e lim								x) =
y ′ = lim							ln (1+
x → 0			x → 0
Loga e lim								loga e.
	x → 0

3.8. Differentiering af en kompleks funktion.

Afledte magt og eksponentielle funktioner

Lad den komplekse funktion y af argumentet x være givet ved formlerne y = f (u),

u = ϕ (x) (se afsnit 1.4.3)

Sætning 3.4 (om den afledede af en sammensat funktion). Hvis funktioner

y = f (u), u = ϕ (x) er differentiable		i de respektive	hinanden
punkterne u og x, derefter den komplekse funktion		f [ϕ (x)] er også differentierbar i
	x, og	y 'x = y 'u u' x.
	y ′ = f ′ (u) u ′ eller
Bevis. Den uafhængige variabel x gives et trin
	x, så får funktionen u = ϕ (x) en stigning u,		hvad vil forårsage

stigningen y af funktionen y = f (u). Da funktionen y = f (u), ved sætningens hypotese, er differentierbar ved det punkt u, der er under overvejelse, kan dens stigning på dette punkt repræsenteres som (se definition 3.4)

			u, hvor α (		u) → o som u → 0.
y = f (u) u + α (u)
				f (u)	x + α (u)
Funktion u = ϕ (x)			differentierbar og dermed kontinuerlig til sagen
ne x svarende til ovenstående punkt u							(Sætning 3.2).
Derfor,				kontinuitet		lim u = 0,	og derfor
						x → 0
lim α (u) = 0.
x → 0
I betragtning af dette,		overgang til			den sidste	ligestilling til	grænse kl

x → 0, kommer vi til (3.18).

Ved at gange lighed (3.18) led for led med dx får vi et udtryk for differentialet af en sammensat funktion

dy = f ′ (u) du.

Kommentar. Differentialet af funktionen y = f (u) ville have nøjagtig samme form, hvis argumentet u ikke var en funktion, men en uafhængig variabel. Dette er den såkaldte invarians egenskab(uafhængighed) af differentialets form med hensyn til argumentet. Man skal huske på, at hvis u er en uafhængig variabel, så er du = u dens vilkårlige stigning, hvis u er et mellemargument (det vil sige en funktion), så er du differentialet af denne funktion, det vil sige en værdi, der ikke falder sammen med dens stigning u.

Ved at bruge den sidste sætning er det nemt at få formler for differentialet

forholdet mellem eksponentiel og eksponentiel funktion:

α−1

2). (en

ln a;

3). (e

1). (x

) = α x

Virkelig,

antager

x> 0,

logaritme begge dele

formlerne y = x α; ln y = α ln x. Her y

Dette er en funktion af x, hvorved

venstre side af den sidste lighed er en kompleks funktion af x. Ved at differentiere begge sider af den sidste lighed med hensyn til x (venstre side som en kompleks funktion), får vi

1 y y ′ = a 1 x,

y ′ = ay x = ax x a = ax a - 1.

Det er let at vise, at dette resultat også er sandt for x< 0 , если только при

denne x α giver mening. Tidligere blev resultatet opnået for tilfældet α = n. Den anden formel opnås på lignende måde, hvorfra i det særlige tilfælde af a = e den sidste formel følger.

Kommentar. Metoden til foreløbig logaritme, som blev brugt til at opnå formlen for differentiering af en potensfunktion, har en selvstændig betydning og kaldes sammen med den efterfølgende fund af den afledede af funktionens logaritme

lnx) "= cosx lnx + sin x x.

Derfor,

y ′ = x sin x (cosx lnx + sin x x)

Kommentar. Reglen om differentiering af en kompleks funktion kan også anvendes til at finde den afledede af en funktion givet implicit.

Faktisk, hvis forholdet mellem x og y er givet på formen F (x, y) = 0, og denne ligning kan løses med hensyn til y, så kan den afledede y ′ findes fra ligningen

					(F (x, y (x)) = 0.
Eksempel 3.4.								y = f (x), givet ikke-
		Find den afledede af en funktion
eksplicit ved ligningen		arctan (y) - y + x = 0.				y som funktion af x:
Vi differentierer ligheden med hensyn til x, forudsat
	y"						1 + år
			- y ′ + 1 = 0, hvorfra			y ′ =
	1 + y 2

3.9. Differentiering af den inverse funktion.

Differentiering af inverse trigonometriske funktioner

Lad der gives to indbyrdes inverse funktioner y = f (x) og x = ϕ (y)

(se punkt 1.4.8).

Sætning 3.5 (om den afledede af den inverse funktion). Hvis funktioner

y = f (x),

x = ϕ (y)

øge (mindske) og i punktet x funktionen f (x)

differentierbar,

f ′ (x) ≠ 0, derefter ved det tilsvarende punkt

funktionen ϕ (y) er også differentierbar (med hensyn til y), og

Bevis.

indstille stigningen

x = ϕ (y)

er stigende

(falder)

x = ϕ (y + y) - ϕ (y) ≠ 0 og

Under sætningens betingelser

x = ϕ (y)

x → 0

y → 0

er kontinuert (sætning 3.2), på grund af hvilket

Første niveau

Afledt af funktionen. Omfattende vejledning (2019)

Forestil dig en lige vej gennem kuperet terræn. Det vil sige, at den går op og ned, men drejer hverken til højre eller venstre. Hvis aksen er rettet langs vejen vandret og - lodret, så vil vejlinjen være meget lig grafen for en kontinuerlig funktion:

Aksen er et vist niveau af nul højde, i livet bruger vi havniveauet som det.

Bevæger vi os fremad ad sådan en vej, bevæger vi os også op eller ned. Vi kan også sige: når argumentet ændres (bevægelse langs abscissen), ændres værdien af ​​funktionen (bevægelse langs ordinaten). Lad os nu tænke på, hvordan man bestemmer "stejlheden" af vores vej? Hvilken slags værdi kan det være? Det er meget enkelt: hvor meget højden vil ændre sig, når man bevæger sig fremad en vis afstand. Faktisk, på forskellige sektioner af vejen, når vi bevæger os fremad (langs abscissen) med en kilometer, vil vi stige eller falde med et andet antal meter i forhold til havniveauet (langs ordinaten).

Vi vil udpege fremadgående bevægelse (det lyder "delta x").

Det græske bogstav (delta) er almindeligt brugt i matematik som et præfiks, der betyder "ændring". Det vil sige - det er en ændring i værdi, - en ændring; hvad er det så? Det er rigtigt, en ændring i størrelsesorden.

Vigtigt: et udtryk er en enkelt helhed, én variabel. Du bør aldrig rive "delta" af "x" eller noget andet bogstav! Det er f.eks.

Så vi har bevæget os fremad, vandret, videre. Hvis vi sammenligner vejlinjen med grafen for en funktion, hvordan betegner vi så stigningen? Selvfølgelig, . Det vil sige, når vi bevæger os fremad, stiger vi højere med.

Det er let at beregne værdien: hvis vi i begyndelsen var i en højde, og efter at have flyttet var vi i en højde, så. Hvis slutpunktet er lavere end startpunktet, vil det være negativt – det betyder, at vi ikke skal op, men ned.

Tilbage til "stejl": dette er en værdi, der angiver, hvor meget (stejlt) højden stiger, når du bevæger dig en afstandsenhed frem:

Antag, at på en del af stien stiger vejen opad med km, når man går frem med km. Så er stejlheden på dette tidspunkt. Og hvis vejen, når man bevægede sig med m, sank med km? Så er hældningen.

Overvej nu toppen af ​​en bakke. Tager man begyndelsen af ​​strækningen en halv kilometer før toppen, og slutningen en halv kilometer efter den, kan man se, at højden er praktisk talt den samme.

Det vil sige, ifølge vores logik viser det sig, at stejlheden her er næsten nul, hvilket tydeligvis ikke er sandt. Det er bare, at meget kan ændre sig på afstand i km. Det er nødvendigt at overveje mindre strækninger for en mere fyldestgørende og præcis vurdering af stejlheden. Hvis du for eksempel måler ændringen i højden, når du bevæger dig en meter, bliver resultatet meget mere præcist. Men selv denne nøjagtighed er måske ikke nok for os - trods alt, hvis der er en stolpe midt på vejen, kan vi simpelthen smutte igennem den. Hvilken afstand vælger vi så? Centimeter? Millimeter? Mindre er bedre!

I det virkelige liv er det mere end nok at måle afstand med millimeter nøjagtighed. Men matematikere stræber altid efter perfektion. Derfor blev konceptet opfundet uendelig lille, det vil sige, at størrelsen er mindre end ethvert tal, vi kan navngive. For eksempel siger du: en billion! Hvor meget mindre? Og du dividerer dette tal med - og det bliver endnu mindre. Etc. Hvis vi vil skrive, at værdien er uendelig lille, skriver vi sådan her: (vi læser "x har en tendens til nul"). Det er meget vigtigt at forstå at dette tal ikke er nul! Men meget tæt på ham. Det betyder, at du kan dividere med det.

Begrebet modsat det uendeligt lille er uendeligt stort (). Du er sandsynligvis allerede stødt ind i det, når du beskæftiger dig med uligheder: dette tal er modulo større end noget tal, du kan komme i tanke om. Hvis du kommer op på det størst mulige tal, skal du bare gange det med to, og du får endnu mere. Og uendeligheden er endnu større end hvad du får. Faktisk er det uendeligt store og det uendeligt lille omvendt til hinanden, altså ved og omvendt: kl.

Lad os nu vende tilbage til vores vej. Den ideelt beregnede hældning er krumningen beregnet for en uendelig lille del af stien, dvs.

Bemærk, at med en uendelig lille forskydning, vil ændringen i højden også være uendelig lille. Men lad mig minde dig om, at uendeligt lille ikke betyder lig med nul. Hvis man dividerer de infinitesimale tal med hinanden, kan man få et helt almindeligt tal f.eks. Det vil sige, at en lille værdi kan være præcis dobbelt så stor som en anden.

Hvad er alt dette til for? Vejen, stejlheden ... Vi skal ikke på motorrally, men vi underviser i matematik. Og i matematik er alt præcis det samme, kun det hedder anderledes.

Afledt koncept

Den afledede af en funktion er forholdet mellem funktionens stigning og stigningen af ​​argumentet ved en uendelig stigning af argumentet.

I trin i matematik kaldes forandring. Hvor meget argumentet () har ændret sig under bevægelse langs aksen kaldes argumentstigning og betegnes I hvor høj grad funktionen (højden) har ændret sig, når man bevæger sig fremad langs aksen med en afstand, kaldes funktionstilvækst og er angivet med.

Så den afledede af en funktion er forholdet til at. Vi betegner den afledede med samme bogstav som funktionen, kun med et primtal øverst til højre: eller simpelthen. Så lad os skrive den afledede formlen ved hjælp af disse notation:

Som i analogien med vejen, her, når funktionen øges, er den afledte positiv, og når funktionen falder, er den negativ.

Er der en afledt lig med nul? Selvfølgelig. For eksempel, hvis vi kører på en flad, vandret vej, er stejlheden nul. Højden ændrer sig faktisk ikke overhovedet. Sådan er det med den afledede: den afledede af en konstant funktion (konstant) er lig med nul:

da stigningen af ​​en sådan funktion er nul for enhver.

Lad os huske eksemplet på en bakketop. Der viste det sig, at det var muligt at arrangere enderne af segmentet på modsatte sider af toppunktet, så højden ved enderne viser sig at være den samme, det vil sige, at segmentet er parallelt med aksen:

Men store strækninger er et tegn på unøjagtig måling. Vi løfter vores segment op parallelt med sig selv, så vil dets længde falde.

Til sidst, når vi er uendeligt tæt på toppen, vil længden af ​​segmentet blive uendeligt lille. Men på samme tid forblev det parallelt med aksen, det vil sige, at forskellen i højder ved dens ender er lig med nul (den tenderer ikke, men den er lige). Derfor derivatet

Du kan forstå det på denne måde: Når vi står helt øverst, ændrer et lille skift til venstre eller højre vores højde ubetydeligt lidt.

Der er også en rent algebraisk forklaring: Til venstre for toppunktet øges funktionen, og til højre falder den. Som vi allerede har fundet ud af tidligere, når funktionen øges, er den afledte positiv, og når funktionen falder, er den negativ. Men det skifter jævnt uden hop (fordi vejen ikke ændrer sin hældning brat nogen steder). Derfor skal der nødvendigvis være mellem negative og positive værdier. Det vil være der, hvor funktionen hverken stiger eller falder - i toppunktet.

Det samme gælder for bunden (det område, hvor funktionen falder til venstre og øges til højre):

Lidt flere detaljer om stigninger.

Så vi ændrer argumentet til værdien. Skift fra hvilken værdi? Hvad er han (argumentet) nu? Vi kan vælge et hvilket som helst punkt, og nu vil vi danse ud fra det.

Overvej et punkt med en koordinat. Værdien af ​​funktionen i den er. Så laver vi den samme stigning: vi øger koordinaten med. Hvad er argumentet nu lig med? Meget let: . Hvad er værdien af ​​funktionen nu? Hvor argumentet går, gør funktionen:. Hvad med funktionstilvæksten? Intet nyt: dette er stadig det beløb, funktionen ændrede med:

Øv dig i at finde trin:

1. Find tilvæksten af ​​funktionen i punktet med argumentet tilvækst lig med.
2. Det samme gælder for funktionen på punktet.

Løsninger:

På forskellige punkter med samme stigning i argumentet, vil stigningen af ​​funktionen være forskellig. Det betyder, at den afledte på hvert punkt er forskellig (vi diskuterede dette i begyndelsen - vejens stejlhed på forskellige punkter er forskellig). Derfor, når vi skriver den afledede, skal vi angive på hvilket tidspunkt:

Power funktion.

En potensfunktion kaldes en funktion, hvor argumentet til en vis grad er (logisk, ikke?).

Og - i ethvert omfang:.

Det enkleste tilfælde er, når eksponenten:

Lad os finde dens afledte på punktet. Lad os huske definitionen af ​​et derivat:

Så argumentet ændres fra til. Hvad er stigningen af ​​funktionen?

Tilvæksten er dette. Men funktionen på ethvert tidspunkt er lig med dens argument. Derfor:

Den afledte er lig med:

Den afledte af er lig med:

b) Overvej nu den kvadratiske funktion ():.

Lad os nu huske det. Dette betyder, at værdien af ​​tilvæksten kan negligeres, da den er uendelig lille og derfor ubetydelig på baggrund af et andet udtryk:

Så vi har den næste regel:

c) Vi fortsætter den logiske række:.

Dette udtryk kan forenkles på forskellige måder: Udvid den første parentes ved hjælp af formlen for forkortet multiplikation af summens terning, eller faktor hele udtrykket ved hjælp af formlen for forskellen mellem terninger. Prøv at gøre det selv på en af ​​de foreslåede måder.

Så jeg endte med følgende:

Og igen, husk det. Det betyder, at du kan forsømme alle vilkårene, der indeholder:

Vi får:.

d) Lignende regler kan opnås for højere grader:

e) Det viser sig, at denne regel kan generaliseres for en potensfunktion med en vilkårlig eksponent, ikke engang et heltal:

(2)

Reglen kan formuleres med ordene: "graden anføres som en koefficient, og så falder den med".

Vi vil bevise denne regel senere (næsten til allersidst). Lad os nu se på et par eksempler. Find den afledede af funktionerne:

1. (på to måder: ved formlen og ved hjælp af definitionen af ​​den afledede - ved at beregne stigningen af ​​funktionen);

1. ... Tro det eller ej, dette er en magtfunktion. Hvis du har spørgsmål som "Hvordan er det her? Og hvor er graden?”, Husk emnet“ ”!
   Ja, roden er også en grad, kun brøk:.
   Så vores kvadratrod er bare en potens med en eksponent:
   .
   Vi leder efter derivatet i henhold til den nyligt lærte formel:

   Hvis det på dette sted bliver uklart igen, gentag emnet "" !!! (om graden med negativ eksponent)

2. ... Nu eksponenten:

   Og nu gennem definitionen (har du glemt det endnu?):
   ;
   .
   Nu, som sædvanlig, forsømmer vi udtrykket, der indeholder:
   .

3. ... En kombination af de tidligere tilfælde:.

Trigonometriske funktioner.

Her vil vi bruge et faktum fra højere matematik:

Når udtryk.

Du lærer beviset i det første år af instituttet (og for at komme dertil skal du bestå eksamen godt). Nu vil jeg bare vise det grafisk:

Vi ser, at funktionen ikke eksisterer - punktet på grafen er punkteret. Men jo tættere på værdien, jo tættere er funktionen. Dette er selve "aspirer".

Derudover kan du kontrollere denne regel ved hjælp af en lommeregner. Ja, ja, vær ikke genert, tag lommeregneren, vi er ikke til eksamen endnu.

Så lad os prøve:;

Glem ikke at sætte lommeregneren i "Radians"-tilstand!

etc. Vi ser, at jo mindre, jo tættere er værdien af ​​forholdet.

a) Overvej funktionen. Lad os som sædvanlig finde dens stigning:

Lad os omdanne forskellen på sinus til et produkt. Til dette bruger vi formlen (husk emnet ""):.

Nu den afledte:

Lad os lave en erstatning:. Så er den for uendelig lille også uendelig lille:. Udtrykket for har formen:

Husk nu, at når udtryk. Og også, hvad nu hvis en uendelig lille mængde kan negligeres i summen (det vil sige ved).

Så vi får følgende regel: sinusafledte er lig med cosinus:

Disse er basis ("tabel") derivater. Her er de på én liste:

Senere vil vi tilføje nogle flere til dem, men disse er de vigtigste, da de bruges oftest.

Øve sig:

1. Find den afledede af funktionen i punktet;
2. Find den afledede af funktionen.

Løsninger:

1. Først finder vi den afledede i generel form og erstatter derefter dens værdi i stedet:
   ;
   .
2. Her har vi noget, der ligner en magtfunktion. Lad os prøve at bringe hende til
   normal visning:
   .
   Godt, nu kan du bruge formlen:
   .
   .
3. ... Eeeeee ... .. Hvad er det her ????

Okay, du har ret, vi ved ikke, hvordan man finder sådanne derivater endnu. Her har vi en kombination af flere typer funktioner. For at arbejde med dem skal du lære nogle flere regler:

Eksponent og naturlig logaritme.

Der er en sådan funktion i matematik, hvis afledte for enhver er lig med værdien af ​​selve funktionen. Det kaldes "eksponentiel", og er en eksponentiel funktion

Grundlaget for denne funktion - en konstant - er en uendelig decimalbrøk, det vil sige et irrationelt tal (såsom). Det kaldes "Eulers nummer", og derfor betegnet med et bogstav.

Så reglen er:

Det er meget nemt at huske.

Nå, lad os ikke gå langt, vi vil straks overveje den omvendte funktion. Hvilken funktion er den inverse af eksponentialfunktionen? Logaritme:

I vores tilfælde er basen et tal:

En sådan logaritme (det vil sige en logaritme med en base) kaldes "naturlig", og vi bruger en speciel notation til den: skriv i stedet.

Hvad er lig med? Selvfølgelig, .

Den afledede af den naturlige logaritme er også meget enkel:

Eksempler:

1. Find den afledede af funktionen.
2. Hvad er den afledede af funktionen?

Svar: Eksponenten og den naturlige logaritme er entydigt simple funktioner set fra den afledede synsvinkel. Eksponentielle og logaritmiske funktioner med enhver anden base vil have en anden afledet, som vi vil analysere senere, efter at vi har gennemgået reglerne for differentiering.

Differentieringsregler

Reglerne for hvad? Igen en ny periode, igen?! ...

Differentiering er processen med at finde et derivat.

Det er alt. Hvordan kan man ellers kalde denne proces med ét ord? Ikke en afledning ... Matematikkens differentiale kaldes den samme stigning af en funktion ved. Dette udtryk kommer fra det latinske differentia - forskel. Her.

Når vi udleder alle disse regler, vil vi bruge to funktioner, for eksempel og. Vi har også brug for formler for deres inkrementer:

Der er i alt 5 regler.

Konstanten flyttes uden for det afledede tegn.

Hvis er et konstant tal (konstant), så.

Denne regel virker naturligvis også for forskellen:.

Lad os bevise det. Lad, eller lettere.

Eksempler.

Find de afledte funktioner:

1. på punktet;
2. på punktet;
3. på punktet;
4. på punktet.

Løsninger:

1. (den afledte er den samme i alle punkter, da det er en lineær funktion, husker du?);

Afledt af et værk

Alt er det samme her: vi introducerer en ny funktion og finder dens stigning:

Afledte:

Eksempler:

1. Find de afledte funktioner og;
2. Find den afledede af funktionen i punktet.

Løsninger:

Afledt af eksponentialfunktionen

Nu er din viden nok til at lære at finde den afledede af enhver eksponentiel funktion, ikke kun eksponenten (har du glemt, hvad det er?).

Så hvor er et tal.

Vi kender allerede den afledede af funktionen, så lad os prøve at støbe vores funktion til en ny radix:

For at gøre dette bruger vi en simpel regel:. Derefter:

Nå, det virkede. Prøv nu at finde den afledede, og glem ikke, at denne funktion er vanskelig.

sket?

Tjek dig selv her:

Formlen viste sig at være meget lig eksponentens afledte: Som det var, forbliver det, dukkede kun en multiplikator op, som kun er et tal, men ikke en variabel.

Eksempler:
Find de afledte funktioner:

Svar:

Dette er blot et tal, der ikke kan beregnes uden en lommeregner, det vil sige, at det ikke kan skrives i en enklere form. Derfor lader vi det i svaret være i denne form.

Afledt af en logaritmisk funktion

Her ligner det: du kender allerede den afledede af den naturlige logaritme:

Derfor, for at finde en vilkårlig en af ​​logaritmen med en anden base, for eksempel:

Du skal bringe denne logaritme til basen. Hvordan ændrer man logaritmens basis? Jeg håber du husker denne formel:

Først nu, i stedet for vil vi skrive:

Nævneren er kun en konstant (konstant tal, ingen variabel). Afledningen er meget enkel:

Afledte af eksponentielle og logaritmiske funktioner findes næsten aldrig i eksamen, men det vil ikke være overflødigt at kende dem.

Afledt af en kompleks funktion.

Hvad er en "kompleks funktion"? Nej, dette er ikke en logaritme og ikke en arctangent. Disse funktioner kan være svære at forstå (selvom hvis logaritmen synes svær for dig, så læs emnet "Logarithms" og alt vil passere), men fra et matematiksynspunkt betyder ordet "svært" ikke "svært".

Forestil dig et lille transportbånd: to personer sidder og laver en form for handling med nogle genstande. For eksempel pakker den første en chokoladebar ind i en indpakning, og den anden binder den med et bånd. Det viser sig sådan en sammensat genstand: en chokoladebar pakket ind og bundet med et bånd. For at spise en chokoladebar skal du udføre de omvendte trin i omvendt rækkefølge.

Lad os skabe en lignende matematisk pipeline: først finder vi cosinus af et tal, og derefter kvadrerer vi det resulterende tal. Så vi får et nummer (chokoladebar), jeg finder dens cosinus (indpakning), og så firkanter du det, jeg har (du binder det med et bånd). Hvad skete der? Fungere. Dette er et eksempel på en kompleks funktion: når vi for at finde dens værdi udfører den første handling direkte med variablen og derefter en anden handling med resultatet af den første.

Vi kan godt gøre de samme handlinger i omvendt rækkefølge: først skal du kvadrere, og så leder jeg efter cosinus af det resulterende tal:. Det er let at gætte, at resultatet næsten altid vil være anderledes. Et vigtigt træk ved komplekse funktioner: Når du ændrer rækkefølgen af ​​handlinger, ændres funktionen.

Med andre ord, en kompleks funktion er en funktion, hvis argument er en anden funktion: .

For det første eksempel.

Andet eksempel: (samme). ...

Den handling, vi laver sidst, vil blive kaldt "Ekstern" funktion, og den handling, der blev taget først - hhv "Intern" funktion(dette er uformelle navne, jeg bruger dem kun til at forklare materialet i et enkelt sprog).

Prøv selv at afgøre, hvilken funktion der er ekstern og hvilken der er intern:

Svar: At adskille indre og ydre funktioner ligner meget at ændre variable: for eksempel i en funktion

1. Hvad er den første handling at tage? Først vil vi beregne sinus, og først derefter hæver vi den til en terning. Det betyder, at det er en intern funktion, men en ekstern.
   Og den oprindelige funktion er deres sammensætning:.
2. Indre:; ekstern:.
   Eksamen:.
3. Indre:; ekstern:.
   Eksamen:.
4. Indre:; ekstern:.
   Eksamen:.
5. Indre:; ekstern:.
   Eksamen:.

vi ændrer variable og får en funktion.

Nå, nu vil vi udvinde vores chokoladebar - se efter et derivat. Fremgangsmåden er altid omvendt: først ser vi efter den afledede af den ydre funktion, derefter gange vi resultatet med den afledede af den indre funktion. I forhold til det originale eksempel ser det sådan ud:

Et andet eksempel:

Så lad os endelig formulere en officiel regel:

Algoritme til at finde den afledede af en kompleks funktion:

Alt ser ud til at være enkelt, ikke?

Lad os tjekke med eksempler:

Løsninger:

1) Intern:;

Ekstern:;

2) Internt:;

(Forsøg bare ikke at reducere nu! Intet kan tages ud under cosinus, husker du?)

3) Intern:;

Ekstern:;

Det er umiddelbart klart, at der er en kompleks funktion på tre niveauer her: Dette er trods alt allerede en kompleks funktion i sig selv, og fra den trækker vi også roden ud, det vil sige, vi udfører den tredje handling (vi putter chokoladen i en indpakning og læg den i en mappe med et bånd). Men der er ingen grund til at være bange: i hvert fald vil vi "pakke ud" denne funktion i samme rækkefølge som normalt: fra slutningen.

Det vil sige, først differentierer vi roden, derefter cosinus og først derefter udtrykket i parentes. Og så formerer vi alt dette.

I sådanne tilfælde er det praktisk at nummerere trinene. Det vil sige, lad os forestille os, hvad vi ved. I hvilken rækkefølge vil vi udføre handlinger for at beregne værdien af ​​dette udtryk? Lad os tage et eksempel:

Jo senere handlingen udføres, jo mere "ekstern" vil den tilsvarende funktion være. Rækkefølgen af ​​handlinger - som før:

Her er indlejring generelt 4-niveau. Lad os definere en fremgangsmåde.

1. Et radikalt udtryk. ...

2. Rod. ...

3. Sinus. ...

4. Firkantet. ...

5. At sætte alt sammen:

AFLEDTE. KORT OM DE VIGTIGSTE

Afledt af en funktion- forholdet mellem stigningen af ​​funktionen og stigningen af ​​argumentet med en uendelig lille stigning af argumentet:

Grundlæggende derivater:

Differentieringsregler:

Konstanten flyttes uden for det afledede tegn:

Afledt af beløbet:

Afledt af værket:

Afledt af kvotienten:

Afledt af en kompleks funktion:

Algoritme til at finde den afledede af en kompleks funktion:

1. Vi definerer den "interne" funktion, vi finder dens afledte.
2. Vi definerer den "eksterne" funktion, vi finder dens afledte.
3. Vi multiplicerer resultaterne af det første og andet punkt.