Piramida. Krnja piramida

Piramida je poliedar, čije je jedno lice mnogougao ( baza ), a sva ostala lica su trokuti sa zajedničkim vrhom ( bočne strane ) (Sl. 15). Piramida se zove ispravan , ako je njegova osnova pravilan mnogougao i vrh piramide je projektovan u centar osnove (Sl. 16). Zove se trouglasta piramida čiji su svi rubovi jednaki tetraedar .

Lateralno rebro piramide je strana bočne strane koja ne pripada osnovici Visina piramida je udaljenost od njenog vrha do ravni baze. Sve bočna rebra pravilne piramide jednake su jedna drugoj, sve bočne strane su jednake jednakokraki trouglovi. Visina bočne strane pravilne piramide povučena iz vrha naziva se apothem . Dijagonalni presjek naziva se presjek piramide ravninom koja prolazi kroz dvije bočne ivice koje ne pripadaju istoj površini.

Bočna površina piramida je zbir površina svih bočnih strana. Ukupna površina naziva se zbir površina svih bočnih strana i baze.

Teoreme

1. Ako su u piramidi sve bočne ivice jednako nagnute prema ravni osnove, tada se vrh piramide projektuje u centar kružnice opisane u blizini baze.

2. Ako su sve bočne ivice piramide jednake dužine, tada se vrh piramide projektuje u centar kružnice opisane blizu osnove.

3. Ako su sva lica u piramidi podjednako nagnuta prema ravni osnove, tada se vrh piramide projektuje u centar kruga upisanog u bazu.

Za izračunavanje zapremine proizvoljne piramide, ispravna formula je:

Gdje V- zapremina;

S baza– bazna površina;

H– visina piramide.

Za pravilnu piramidu ispravne su sljedeće formule:

Gdje str– perimetar baze;

h a– apotema;

H- visina;

S puna

S strana

S baza– bazna površina;

V– zapremina pravilne piramide.

Krnja piramida naziva se dio piramide zatvoren između osnove i rezne ravni paralelne sa osnovom piramide (slika 17). Pravilna skraćena piramida naziva se dio pravilne piramide zatvoren između osnove i rezne ravni paralelne s osnovom piramide.

Grounds skraćena piramida - slični poligoni. Bočne strane – trapezi. Visina krnje piramide je rastojanje između njenih osnova. Dijagonala skraćena piramida je segment koji povezuje njene vrhove koji ne leže na istoj površini. Dijagonalni presjek je presjek skraćene piramide ravninom koja prolazi kroz dvije bočne ivice koje ne pripadaju istoj površini.

Za skraćenu piramidu važe sljedeće formule:

(4)

Gdje S 1 , S 2 – površine gornje i donje osnove;

S puna– ukupna površina;

S strana– bočna površina;

H- visina;

V– zapremina krnje piramide.

Za pravilnu skraćenu piramidu formula je tačna:

Gdje str 1 , str 2 – perimetri osnova;

h a– apotema pravilne krnje piramide.

Primjer 1. U pravilnoj trouglastoj piramidi, ugao diedara u osnovi je 60º. Pronađite tangentu ugla nagiba bočne ivice prema ravni baze.

Rješenje. Napravimo crtež (slika 18).

Piramida je pravilna, što znači da se u osnovi nalazi jednakostranični trougao, a sve bočne strane su jednaki jednakokraki trouglovi. Diedarski ugao u osnovi je ugao nagiba bočne strane piramide prema ravni osnove. Linearni ugao je ugao a između dvije okomice: itd. Vrh piramide projektovan je u centar trougla (središte opisane i upisane kružnice trokuta ABC). Ugao nagiba bočne ivice (npr S.B.) je ugao između samog ruba i njegove projekcije na ravan baze. Za rebro S.B. ovaj ugao će biti ugao SBD. Da biste pronašli tangentu, morate znati noge SO I O.B.. Neka je dužina segmenta BD jednako 3 A. Dot O linijski segment BD je podijeljen na dijelove: i Od nalazimo SO: Od nalazimo:

odgovor:

Primjer 2. Nađite zapreminu pravilne skraćene četvorougaone piramide ako su dijagonale njenih osnova jednake cm i cm, a visina 4 cm.

Rješenje. Da bismo pronašli zapreminu krnje piramide, koristimo formulu (4). Da biste pronašli površinu baza, morate pronaći stranice osnovnih kvadrata, znajući njihove dijagonale. Stranice osnovica su jednake 2 cm odnosno 8 cm.To znači površine osnova i Zamjenom svih podataka u formulu izračunavamo zapreminu krnje piramide:

odgovor: 112 cm 3.

Primjer 3. Nađite površinu bočne strane pravilne trokutaste skraćene piramide čije su stranice osnova 10 cm i 4 cm, a visina piramide 2 cm.

Rješenje. Napravimo crtež (slika 19).

Bočna strana ove piramide je jednakokraki trapez. Da biste izračunali površinu trapeza, morate znati osnovu i visinu. Osnove su date prema uslovu, samo visina ostaje nepoznata. Naći ćemo je odakle A 1 E okomito iz tačke A 1 na ravni donje baze, A 1 D– okomito od A 1 per AC. A 1 E= 2 cm, jer je ovo visina piramide. Naći DE Napravimo dodatni crtež koji prikazuje pogled odozgo (slika 20). Dot O– projekcija centara gornje i donje baze. budući da (vidi sliku 20) i S druge strane uredu– radijus upisan u krug i OM– radijus upisan u krug:

MK = DE.

Prema Pitagorinoj teoremi iz

Bočna površina lica:

odgovor:

Primjer 4. U osnovi piramide leži jednakokraki trapez, čije su osnove A I b (a> b). Svaka bočna strana formira ugao jednak ravni osnove piramide j. Pronađite ukupnu površinu piramide.

Rješenje. Napravimo crtež (slika 21). Ukupna površina piramide SABCD jednak zbroju površina i površine trapeza A B C D.

Upotrijebimo tvrdnju da ako su sva lica piramide podjednako nagnuta prema ravni baze, tada se vrh projektuje u središte kruga upisanog u bazu. Dot O– projekcija temena S u osnovi piramide. Trougao SOD je ortogonalna projekcija trougla CSD do ravni baze. Po teoremi o površini ortogonalna projekcija ravnu cifru dobijamo:

Isto tako znači Dakle, problem se sveo na pronalaženje površine trapeza A B C D. Nacrtajmo trapez A B C D odvojeno (sl. 22). Dot O– središte kruga upisanog u trapez.

Kako se kružnica može upisati u trapez, onda ili Iz Pitagorine teoreme imamo

Prvi nivo

Piramida. Vizuelni vodič (2019)

Šta je piramida?

Kako ona izgleda?

Vidite: na dnu piramide (kažu “ u bazi") neki poligon, a svi vrhovi ovog poligona su povezani sa nekom tačkom u prostoru (ova tačka se zove " vertex»).

Cijela ova struktura još uvijek postoji bočne strane, bočna rebra I bazna rebra. Još jednom, nacrtajmo piramidu zajedno sa svim ovim imenima:

Neke piramide mogu izgledati vrlo čudno, ali one su i dalje piramide.

Ovdje je, na primjer, potpuno "koso" piramida.

I još malo o nazivima: ako je u podnožju piramide trokut, onda se piramida zove trokutna, ako je četverokut, onda je četverokut, a ako je petougao, onda... pogodite sami .

Istovremeno, tačka gde je pao visina, zvao visina osnove. Imajte na umu da u "krivim" piramidama visina može čak završiti izvan piramide. Volim ovo:

I nema ništa loše u tome. Izgleda kao tupougao.

Ispravna piramida.

Puno složene riječi? Hajde da dešifrujemo: "U osnovi - tačno" - to je razumljivo. Sada hajde da zapamtimo da regularni poligon ima centar - tačka koja je centar i , I .

Pa, riječi "vrh je projektovan u centar baze" znače da osnova visine pada tačno u centar baze. Pogledajte kako izgleda glatko i slatko pravilne piramide.

Hexagonal: u osnovi je pravilan šestougao, vrh je projektovan u centar baze.

Quadrangular: osnova je kvadrat, vrh je projektovan na tačku preseka dijagonala ovog kvadrata.

Triangular: u osnovi je pravilan trougao, vrh je projektovan na tačku preseka visina (one su i medijane i simetrale) ovog trougla.

Veoma važna svojstva ispravna piramida:

U desnoj piramidi

• sve bočne ivice su jednake.
• sve bočne strane su jednakokraki trouglovi i svi ti trokuti su jednaki.

Volumen piramide

Glavna formula za volumen piramide:

Odakle je to tačno došlo? Ovo nije tako jednostavno, i u početku samo trebate zapamtiti da piramida i konus imaju volumen u formuli, ali cilindar ne.

Sada izračunajmo zapreminu najpopularnijih piramida.

Neka je stranica osnove jednaka, a bočna ivica jednaka. Moramo pronaći i.

Ovo je površina pravilnog trougla.

Prisjetimo se kako tražiti ovo područje. Koristimo formulu površine:

Za nas je “ ” ovo, a “ ” je također ovo, eh.

Sad hajde da ga nađemo.

Prema Pitagorinoj teoremi za

Koja je razlika? Ovo je radijus kruga u jer piramidaispravan a samim tim i centar.

Pošto - i tačka preseka medijana.

(Pitagorina teorema za)

Zamijenimo ga u formulu za.

I zamijenimo sve u formulu volumena:

pažnja: ako imate pravilan tetraedar (tj.), onda formula ispada ovako:

Neka je stranica osnove jednaka, a bočna ivica jednaka.

Nema potrebe tražiti ovdje; Na kraju krajeva, baza je kvadrat, i stoga.

Naći ćemo ga. Prema Pitagorinoj teoremi za

Da li znamo? Skoro. pogledajte:

(vidjeli smo to gledajući).

Zamijenite u formulu za:

A sada zamjenjujemo i u formulu volumena.

Neka je stranica osnove jednaka i bočna ivica.

Kako pronaći? Gledajte, šestougao se sastoji od tačno šest identičnih pravilnih trouglova. Već smo tražili površinu pravilnog trokuta pri izračunavanju volumena pravilne trokutaste piramide; ovdje koristimo formulu koju smo pronašli.

Sada hajde da pronađemo (to).

Prema Pitagorinoj teoremi za

Ali kakve to veze ima? Jednostavno je jer je (i svi ostali također) u pravu.

Zamenimo:

\displaystyle V=\frac(\sqrt(3))(2)((a)^(2))\sqrt(((b)^(2))-((a)^(2)))

PIRAMIDA. UKRATKO O GLAVNIM STVARIMA

Piramida je poliedar koji se sastoji od bilo kojeg ravnog mnogougla (), tačke koja ne leži u ravni osnove (vrh piramide) i svih segmenata koji povezuju vrh piramide sa tačkama osnove (bočnim ivicama).

Okomita pala sa vrha piramide na ravan osnove.

Ispravna piramida- piramida u kojoj u osnovi leži pravilan poligon, a vrh piramide je projektovan u centar osnove.

Svojstvo pravilne piramide:

• U pravilnoj piramidi, sve bočne ivice su jednake.
• Sve bočne strane su jednakokraki trokuti i svi ti trokuti su jednaki.

Definicija

Piramida je poliedar sastavljen od poligona \(A_1A_2...A_n\) i \(n\) trokuta sa zajedničkim vrhom \(P\) (koji ne leži u ravni poligona) i stranica nasuprot njemu, koje se poklapaju sa strane poligona.
Oznaka: \(PA_1A_2...A_n\) .
Primjer: pentagonalna piramida \(PA_1A_2A_3A_4A_5\) .

Trokuti \(PA_1A_2, \PA_2A_3\), itd. su pozvani bočne strane piramide, segmenti \(PA_1, PA_2\), itd. – bočna rebra, poligon \(A_1A_2A_3A_4A_5\) – osnovu, tačka \(P\) – top.

Visina piramide su okomite koje se spuštaju od vrha piramide do ravni baze.

Zove se piramida sa trouglom u osnovi tetraedar.

Piramida se zove ispravan, ako je njegova osnova pravilan poligon i ako je ispunjen jedan od sljedećih uslova:

\((a)\) bočne ivice piramide su jednake;

\((b)\) visina piramide prolazi kroz centar kružnice opisane u blizini baze;

\((c)\) bočna rebra su nagnuta prema ravni baze pod istim uglom.

\((d)\) bočne strane su nagnute prema ravni baze pod istim uglom.

Regularni tetraedar je trouglasta piramida, čija su sva lica jednaki jednakostranični trouglovi.

Teorema

Uslovi \((a), (b), (c), (d)\) su ekvivalentni.

Dokaz

Nađimo visinu piramide \(PH\) . Neka je \(\alpha\) ravan osnove piramide.

1) Dokažimo da iz \((a)\) slijedi \((b)\) . Neka \(PA_1=PA_2=PA_3=...=PA_n\) .

Jer \(PH\perp \alpha\), tada je \(PH\) okomito na bilo koju pravu koja leži u ovoj ravni, što znači da su trouglovi pravokutni. To znači da su ovi trokuti jednaki u zajedničkom kraku \(PH\) i hipotenuzi \(PA_1=PA_2=PA_3=...=PA_n\) . To znači \(A_1H=A_2H=...=A_nH\) . To znači da su tačke \(A_1, A_2, ..., A_n\) na istoj udaljenosti od tačke \(H\), dakle, leže na istoj kružnici poluprečnika \(A_1H\) . Ovaj krug je, po definiciji, opisan oko poligona \(A_1A_2...A_n\) .

2) Dokažimo da \((b)\) implicira \((c)\) .

\(PA_1H, PA_2H, PA_3H,..., PA_nH\) pravougaona i jednaka na dvije noge. To znači da su i njihovi uglovi jednaki, dakle, \(\ugao PA_1H=\ugao PA_2H=...=\ugao PA_nH\).

3) Dokažimo da \((c)\) implicira \((a)\) .

Slično prvoj tački, trouglovi \(PA_1H, PA_2H, PA_3H,..., PA_nH\) pravougaona i duž kraka i oštrog ugla. To znači da su i njihove hipotenuze jednake, odnosno \(PA_1=PA_2=PA_3=...=PA_n\) .

4) Dokažimo da \((b)\) implicira \((d)\) .

Jer u pravilnom poligonu centri opisane i upisane kružnice se poklapaju (općenito govoreći, ova tačka se naziva središtem pravilnog mnogougla), tada je \(H\) centar upisane kružnice. Nacrtajmo okomite iz tačke \(H\) na stranice baze: \(HK_1, HK_2\), itd. Ovo su poluprečnici upisane kružnice (po definiciji). Zatim, prema TTP (\(PH\) je okomita na ravan, \(HK_1, HK_2\), itd. su projekcije okomite na stranice) nagnute \(PK_1, PK_2\) itd. okomito na stranice \(A_1A_2, A_2A_3\), itd. respektivno. Dakle, po definiciji \(\ugao PK_1H, \ugao PK_2H\) jednak uglovima između bočnih strana i baze. Jer trokuti \(PK_1H, PK_2H, ...\) su jednaki (kao pravougaoni sa dve strane), zatim uglovi \(\ugao PK_1H, \ugao PK_2H, ...\) su jednaki.

5) Dokažimo da \((d)\) implicira \((b)\) .

Slično četvrtoj tački, trokuti \(PK_1H, PK_2H, ...\) su jednaki (kao pravougaoni duž kraka i oštri ugao), što znači da su segmenti \(HK_1=HK_2=...=HK_n\) jednaka. To znači, po definiciji, \(H\) je centar kružnice upisane u bazu. Ali zato Za pravilne poligone, centri upisanog i opisanog kruga se poklapaju, tada je \(H\) centar opisane kružnice. Chtd.

Posljedica

Bočne strane pravilne piramide su jednaki jednakokraki trouglovi.

Definicija

Visina bočne strane pravilne piramide povučena iz njenog vrha naziva se apothem.
Apoteme svih bočnih strana pravilne piramide su jednake jedna drugoj i također su medijane i simetrale.

Važne napomene

1. Visina pravilne trouglaste piramide pada u tački preseka visina (ili simetrala, ili medijana) osnove (osnova je pravilan trougao).

2. Visina pravilne četvorougaone piramide pada u tački preseka dijagonala osnove (osnova je kvadrat).

3. Visina pravilne šestougaone piramide pada u tački preseka dijagonala osnove (osnova je pravilan šestougao).

4. Visina piramide je okomita na bilo koju pravu liniju koja leži u osnovi.

Definicija

Piramida se zove pravougaona, ako je jedan od njegovih bočnih rubova okomit na ravan baze.

Važne napomene

1. U pravougaonoj piramidi, ivica okomita na osnovu je visina piramide. To jest, \(SR\) je visina.

2. Jer \(SR\) je onda okomito na bilo koju pravu od baze \(\trokut SRM, \trokut SRP\)– pravougli trouglovi.

3. Trokuti \(\trokut SRN, \trokut SRK\)- takođe pravougaone.
Odnosno, bilo koji trokut formiran od ove ivice i dijagonale koja izlazi iz vrha ovog ruba koji leži u osnovi bit će pravokutni.

\[(\Large(\text(Zapremina i površina piramide)))\]

Teorema

Zapremina piramide jednaka je jednoj trećini proizvoda površine baze i visine piramide: \

Posljedice

Neka je \(a\) stranica baze, \(h\) visina piramide.

1. Zapremina pravilne trouglaste piramide je \(V_(\text(pravougli trokut.pir.))=\dfrac(\sqrt3)(12)a^2h\),

2. Zapremina pravilne četvorougaone piramide je \(V_(\text(right.four.pir.))=\dfrac13a^2h\).

3. Zapremina pravilne šestougaone piramide je \(V_(\text(right.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).

4. Zapremina pravilnog tetraedra je \(V_(\text(desni tetr.))=\dfrac(\sqrt3)(12)a^3\).

Teorema

Površina bočne površine pravilne piramide jednaka je poluproizvodu perimetra osnove i apoteme.

\[(\Large(\text(Frustum)))\]

Definicija

Razmotrimo proizvoljnu piramidu \(PA_1A_2A_3...A_n\) . Povučemo ravan paralelnu sa osnovom piramide kroz određenu tačku koja leži na bočnoj ivici piramide. Ova ravan će podijeliti piramidu na dva poliedra, od kojih je jedan piramida (\(PB_1B_2...B_n\)), a drugi se zove krnje piramide(\(A_1A_2...A_nB_1B_2...B_n\) ).

Skraćena piramida ima dvije osnove - poligone \(A_1A_2...A_n\) i \(B_1B_2...B_n\) koje su međusobno slične.

Visina skraćene piramide je okomica povučena iz neke tačke gornje osnove na ravan donje osnove.

Važne napomene

1. Sve bočne strane krnje piramide su trapezi.

2. Segment koji povezuje centre osnova pravilne krnje piramide (tj. piramide dobijene poprečnim presjekom pravilne piramide) je visina.

Kod kojih je jedno od bočnih rebara okomito na bazu.

U ovom slučaju, ova ivica će biti visina piramide.

Svojstva piramide.

1. Kada sve bočne ivice imaju istu veličinu, tada:

• lako je opisati krug blizu osnove piramide, a vrh piramide će biti projektovan u centar ovog kruga;
• bočna rebra formiraju jednake uglove sa ravninom osnove;
• Štaviše, tačno je i suprotno, tj. kada bočna rebra formiraju jednake uglove sa ravninom osnove, ili kada se krug može opisati oko osnove piramide i vrh piramide će biti projektovan u centar ove kružnice, to znači da su sve bočne ivice piramide su iste veličine.

2. Kada bočne strane imaju ugao nagiba prema ravni osnove iste vrijednosti, tada:

• lako je opisati krug blizu osnove piramide, a vrh piramide će biti projektovan u centar ovog kruga;
• visine bočnih strana su jednake dužine;
• površina bočne površine jednaka je ½ umnoška opsega baze i visine bočne površine.

3. Sfera se može opisati oko piramide ako se u osnovi piramide nalazi poligon oko kojeg se može opisati krug (nužan i dovoljan uslov). Središte sfere će biti tačka presjeka ravnina koje prolaze kroz sredine ivica piramide okomitih na njih. Iz ove teoreme zaključujemo da se sfera može opisati i oko bilo koje trouglaste i oko bilo koje pravilne piramide;

4. Sfera se može upisati u piramidu ako se simetralne ravni unutrašnjih diedarskih uglova piramide seku u 1. tački (neophodan i dovoljan uslov). Ova tačka će postati centar sfere.

5. Konus će biti upisan u piramidu kada im se vrhovi poklope, a osnova konusa će biti upisana u bazu piramide. U ovom slučaju, konus je moguće uklopiti u piramidu samo ako su apotemi piramide jednake veličine (nužan i dovoljan uslov);

6. Konus će biti opisan u blizini piramide ako im se vrhovi poklapaju, a osnova konusa će biti opisana blizu osnove piramide. U ovom slučaju, konus je moguće opisati u blizini piramide samo ako svi bočni rubovi piramide imaju iste vrijednosti (nužan i dovoljan uvjet). Visine ovih čunjeva i piramida su iste.

7. Cilindar će biti upisan u piramidu ako se jedna od njegovih osnova poklapa sa kružnicom koja je u presjek piramide upisana ravninom koja je paralelna osnovici, a druga baza pripada osnovici piramide.

8. Cilindar će biti opisan u blizini piramide kada vrh piramide pripada jednoj od njenih baza, a druga baza cilindra će biti opisana blizu osnove piramide. U ovom slučaju je moguće opisati cilindar u blizini piramide samo ako je osnova piramide upisani poligon (nužan i dovoljan uslov).

Formule za određivanje volumena i površine pravokutne piramide.

V- zapremina piramide,

S- površina osnove piramide,

h- visina piramide,

Sb- površina bočne površine piramide,

a- apotema (ne brkati sa α ) piramide,

P- perimetar osnove piramide,

n- broj stranica osnove piramide,

b- dužina bočne ivice piramide,

α - ravan ugao na vrhu piramide.

Koncept piramide

Definicija 1

Geometrijska figura koju čine poligon i tačka koja ne leži u ravni koja sadrži ovaj poligon, povezana sa svim vrhovima poligona, naziva se piramida (slika 1).

Poligon od kojeg je napravljena piramida naziva se osnova piramide; rezultirajući trokuti, kada su spojeni u tačku, su bočne strane piramide, stranice trokuta su stranice piramide, a tačka zajednička svim trouglovima je vrh piramide.

Vrste piramida

U zavisnosti od broja uglova u osnovi piramide, može se nazvati trouglastim, četvorougaonim i tako dalje (slika 2).

Slika 2.

Druga vrsta piramide je redovna piramida.

Hajde da uvedemo i dokažemo svojstvo pravilne piramide.

Teorema 1

Sve bočne strane pravilne piramide su jednakokraki trouglovi koji su međusobno jednaki.

Dokaz.

Razmotrimo pravilnu $n-$gonalnu piramidu sa vrhom $S$ visine $h=SO$. Nacrtajmo krug oko baze (slika 4).

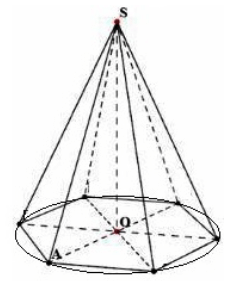
Slika 4.

Razmotrimo trougao $SOA$. Prema Pitagorinoj teoremi, dobijamo

Očigledno, svaka bočna ivica će biti definirana na ovaj način. Prema tome, sve bočne ivice su međusobno jednake, odnosno sve bočne strane su jednakokraki trouglovi. Dokažimo da su oni međusobno jednaki. Pošto je osnova pravilan mnogougao, osnove svih bočnih strana su jedna drugoj. Prema tome, sve bočne strane su jednake prema III kriterijumu jednakosti trouglova.

Teorema je dokazana.

Hajde da sada uvedemo sljedeću definiciju koja se odnosi na koncept pravilne piramide.

Definicija 3

Apotem pravilne piramide je visina njene bočne strane.

Očigledno, prema teoremi jedan, sve apoteme su jedna drugoj jednake.

Teorema 2

Bočna površina pravilne piramide određena je kao proizvod poluperimetra osnove i apoteme.

Dokaz.

Označimo stranu osnove $n-$gonalne piramide sa $a$, a apotemu sa $d$. Dakle, površina bočne strane je jednaka

Pošto su, prema teoremi 1, sve strane jednake, onda

Teorema je dokazana.

Druga vrsta piramide je skraćena piramida.

Definicija 4

Ako se kroz običnu piramidu povuče ravan paralelna njenoj osnovici, onda se lik formiran između ove ravni i ravni osnove naziva krnjom piramidom (slika 5).

Slika 5. Krnja piramida

Bočne strane krnje piramide su trapezi.

Teorema 3

Bočna površina pravilne skraćene piramide određena je kao proizvod zbira poluperimetara baza i apoteme.

Dokaz.

Označimo stranice osnova $n-$gonalne piramide sa $a\ i\ b$, respektivno, a apotemu sa $d$. Dakle, površina bočne strane je jednaka

Pošto su sve strane jednake, onda

Teorema je dokazana.

Primer zadatka

Primjer 1

Nađite površinu bočne površine skraćene trokutaste piramide ako se ona dobije iz pravilne piramide sa osnovnom stranom 4 i apotemom 5 odsijecanjem ravnine koja prolazi kroz srednju liniju bočnih strana.

Rješenje.

Po teoremi o srednja linija mi to shvatamo top base skraćena piramida je jednaka $4\cdot \frac(1)(2)=2$, a apotema je jednaka $5\cdot \frac(1)(2)=2.5$.

Tada, prema teoremi 3, dobijamo