Operasjonen med å finne den deriverte kalles differensiering.

Som et resultat av å løse problemer med å finne deriverte av de enkleste (og ikke veldig enkle) funksjonene ved å definere den deriverte som grensen for forholdet mellom økningen og økningen av argumentet, dukket det opp en tabell med deriverte og nøyaktig visse regler differensiering. De første som arbeidet med å finne derivater var Isaac Newton (1643-1727) og Gottfried Wilhelm Leibniz (1646-1716).

Derfor, i vår tid, for å finne den deriverte av en funksjon, trenger du ikke å beregne den ovennevnte grensen for forholdet mellom økningen av funksjonen og økningen av argumentet, men du trenger bare å bruke tabellen med derivater og differensieringsreglene. Følgende algoritme er egnet for å finne den deriverte.

For å finne den deriverte, trenger du et uttrykk under primtegnet bryte ned enkle funksjoner i komponenter og bestemme hvilke handlinger (produkt, sum, kvotient) disse funksjonene er relatert. Deretter finner vi de deriverte av elementære funksjoner i tabellen over deriverte, og formlene for de deriverte av produktet, sum og kvotient - i differensieringsreglene. Den deriverte tabellen og differensieringsreglene er gitt etter de to første eksemplene.

Eksempel 1. Finn den deriverte av en funksjon

Løsning. Fra differensieringsreglene finner vi ut at den deriverte av en sum av funksjoner er summen av deriverte av funksjoner, dvs.

Fra tabellen over deriverte finner vi ut at den deriverte av "x" er lik en, og den deriverte av sinus er lik cosinus. Vi erstatter disse verdiene i summen av deriverte og finner den deriverte som kreves av tilstanden til problemet:

Eksempel 2. Finn den deriverte av en funksjon

Løsning. Vi differensierer som en derivert av en sum der det andre leddet har en konstant faktor den kan tas ut av tegnet til den deriverte:

Hvis det likevel dukker opp spørsmål om hvor noe kommer fra, blir de vanligvis ryddet opp etter å ha satt seg inn i tabellen over derivater og de enkleste differensieringsreglene. Vi går videre til dem akkurat nå.

Tabell over deriverte av enkle funksjoner

1. Derivert av en konstant (tall). Et hvilket som helst tall (1, 2, 5, 200...) som er i funksjonsuttrykket. Alltid lik null. Dette er veldig viktig å huske, da det kreves veldig ofte
2. Derivert av den uavhengige variabelen. Oftest "X". Alltid lik en. Dette er også viktig å huske lenge
3. Avledet av grad. Når du løser problemer, må du konvertere ikke-kvadratrøtter til potenser.
4. Derivert av en variabel i potensen -1
5. Avledet av kvadratrot
6. Derivert av sinus
7. Derivat av cosinus
8. Derivert av tangent
9. Derivat av cotangens
10. Derivat av arcsine
11. Derivat av arccosine
12. Derivat av arctangens
13. Derivat av lysbue cotangens
14. Derivert av den naturlige logaritmen
15. Derivert av en logaritmisk funksjon
16. Derivert av eksponenten
17. Derivert av en eksponentiell funksjon

Regler for differensiering

1. Derivert av en sum eller differanse
2. Derivat av produktet
2a. Derivert av et uttrykk multiplisert med en konstant faktor
3. Derivat av kvotienten
4. Derivat av en kompleks funksjon

Regel 1.Hvis funksjonene

er differensierbare på et tidspunkt, så er funksjonene differensierbare på samme punkt

og

de. den deriverte av en algebraisk sum av funksjoner er lik den algebraiske summen av de deriverte av disse funksjonene.

Konsekvens. Hvis to differensierbare funksjoner er forskjellige med et konstant ledd, er deres deriverte like, dvs.

Regel 2.Hvis funksjonene

er differensierbare på et tidspunkt, så er produktet deres differensierbart på samme punkt

og

de. Den deriverte av produktet av to funksjoner er lik summen av produktene til hver av disse funksjonene og den deriverte av den andre.

Konsekvens 1. Konstantfaktoren kan tas ut av tegnet til den deriverte:

Konsekvens 2. Den deriverte av produktet av flere differensierbare funksjoner er lik summen av produktene av den deriverte av hver faktor og alle de andre.

For eksempel for tre multiplikatorer:

Regel 3.Hvis funksjonene

differensierbar på et tidspunkt Og , så på dette punktet er kvotienten deres også differensierbaru/v , og

de. den deriverte av kvotienten av to funksjoner er lik en brøk, hvis teller er forskjellen mellom produktene av nevneren og den deriverte av telleren og telleren og den deriverte av nevneren, og nevneren er kvadratet av den tidligere telleren.

Hvor du kan se etter ting på andre sider

Når man finner derivatet til et produkt og en kvotient i reelle problemer, er det alltid nødvendig å bruke flere differensieringsregler samtidig, så det er flere eksempler på disse derivatene i artikkelen"Derivat av produktet og kvotient av funksjoner".

Kommentar. Du bør ikke forveksle en konstant (det vil si et tall) som et ledd i en sum og som en konstant faktor! Når det gjelder et ledd, er dens deriverte lik null, og når det gjelder en konstant faktor, tas den ut av tegnet til de deriverte. Dette typisk feil, som skjer på det første stadiet studere derivater, men ettersom de løser flere en- og todelte eksempler, gjør ikke den gjennomsnittlige eleven lenger denne feilen.

Og hvis du, når du skiller et produkt eller kvotient, har et begrep u"v, hvori u- et tall, for eksempel 2 eller 5, det vil si en konstant, så vil den deriverte av dette tallet være lik null, og derfor vil hele leddet være lik null (dette tilfellet er diskutert i eksempel 10).

Annen vanlig feil- mekanisk løsning av den deriverte av en kompleks funksjon som en derivert av en enkel funksjon. Derfor avledet av en kompleks funksjon en egen artikkel er viet. Men først skal vi lære å finne derivater enkle funksjoner.

Underveis kan du ikke gjøre uten å transformere uttrykk. For å gjøre dette må du kanskje åpne manualen i nye vinduer. Handlinger med krefter og røtter Og Operasjoner med brøker .

Hvis du leter etter løsninger på deriverte av brøker med potenser og røtter, det vil si når funksjonen ser ut som , og følg deretter leksjonen "Avledet av summer av brøker med potenser og røtter."

Hvis du har en oppgave som , så vil du ta leksjonen "Derivater av enkle trigonometriske funksjoner".

Steg-for-trinn eksempler - hvordan finne den deriverte

Eksempel 3. Finn den deriverte av en funksjon

Løsning. Vi definerer delene av funksjonsuttrykket: hele uttrykket representerer et produkt, og dets faktorer er summer, i det andre inneholder ett av leddene en konstant faktor. Vi bruker produktdifferensieringsregelen: den deriverte av produktet av to funksjoner er lik summen av produktene til hver av disse funksjonene med den deriverte av den andre:

Deretter bruker vi regelen for differensiering av summen: den deriverte av den algebraiske summen av funksjoner er lik den algebraiske summen av de deriverte av disse funksjonene. I vårt tilfelle har det andre leddet et minustegn i hver sum. I hver sum ser vi både en uavhengig variabel, hvis deriverte er lik én, og en konstant (tall), hvis deriverte er lik null. Så, "X" blir til en, og minus 5 blir til null. I det andre uttrykket multipliseres "x" med 2, så vi multipliserer to med samme enhet som den deriverte av "x". Vi får følgende deriverte verdier:

Vi erstatter de funnet deriverte i summen av produkter og får den deriverte av hele funksjonen som kreves av tilstanden til problemet:

Eksempel 4. Finn den deriverte av en funksjon

Løsning. Vi er pålagt å finne den deriverte av kvotienten. Vi bruker formelen for å differensiere kvotienten: den deriverte av kvotienten til to funksjoner er lik en brøk, hvis teller er forskjellen mellom produktene til nevneren og den deriverte av telleren og telleren og den deriverte av nevneren, og nevneren er kvadratet til den tidligere telleren. Vi får:

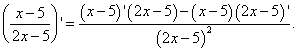
Vi har allerede funnet den deriverte av faktorene i telleren i eksempel 2. La oss heller ikke glemme at produktet, som er den andre faktoren i telleren i gjeldende eksempel, er tatt med et minustegn:

Hvis du leter etter løsninger på problemer der du trenger å finne den deriverte av en funksjon, hvor det er en kontinuerlig haug med røtter og potenser, som f.eks. , så velkommen til timen "Derivat av summer av brøker med potenser og røtter" .

Hvis du trenger å lære mer om derivatene av sinus, cosinus, tangenter og andre trigonometriske funksjoner, det vil si når funksjonen ser ut , så en leksjon for deg "Derivater av enkle trigonometriske funksjoner" .

Eksempel 5. Finn den deriverte av en funksjon

Løsning. I denne funksjonen ser vi et produkt, en av faktorene som er Kvadratrot fra den uavhengige variabelen, den deriverte som vi har sett i tabellen over deriverte. Ved å bruke regelen for å skille produktet og tabellverdien til den deriverte av kvadratroten, får vi:

Eksempel 6. Finn den deriverte av en funksjon

Løsning. I denne funksjonen ser vi en kvotient hvis utbytte er kvadratroten av den uavhengige variabelen. Ved å bruke regelen for differensiering av kvotienter, som vi gjentok og brukte i eksempel 4, og den tabulerte verdien av den deriverte av kvadratroten, får vi:

For å bli kvitt en brøk i telleren, multipliser telleren og nevneren med .

Spørsmål til eksamen akademisk disiplin"Elementer av høyere matematikk"

for spesialitet 230115 "Programmering i datasystemer"

2012\2013 studieår.

Matriser og operasjoner på dem.

(OM. En nullmatrise er en matrise hvis elementer alle er lik 0.

OM. To matriser med samme dimensjon mxn kalles lik, hvis i krysset i-te linje og den j-te kolonnen i den ene og den andre matrisen inneholder samme nummer; i=1, 2, ..., m; j=1, 2, ..., n .

La EN= (a ij) er en matrise og g er et vilkårlig tall, deretter g EN= (g a ij), det vil si at når matrise A multipliseres med tallet g, multipliseres alle tallene som utgjør matrisen A med tallet g.

La A og B være matriser med samme dimensjon A = (a ij), B = (b ij), så er summen deres A + B matrisen C = (c ij) av samme dimensjon, bestemt fra formelen c ij = a ij + b ij, det vil si at når man legger til to matriser, legges tallene som er identisk plassert i dem sammen i par.

Matrise A kan multipliseres med matrise B, det vil si at matrise C = AB kan bli funnet hvis antall kolonner n i matrise A er lik antall rader i matrise B, og matrise C vil ha like mange rader som matrise A har rader og like mange kolonner som matrise har kolonner B. Hvert element i matrise C er definert av en formel.

Element c ij i produktmatrisen C er lik summen av produktene til elementene i i-raden til den første faktormatrisen med de tilsvarende elementene i den j-te kolonnen i den andre faktormatrisen.

Konseptet med en determinant og dens egenskaper.

Dette begrepet har andre betydninger, se Determinant (verdier) .

Avgjørende faktor(eller avgjørende faktor) - et av de grunnleggende konseptene lineær algebra. Avgjørende faktor matriser er polynom fra elementene i en kvadratisk matrise (det vil si en der antallet rader og kolonner er likt). Generelt matrise kan defineres over en hvilken som helst kommutativ ringe, i dette tilfellet vil determinanten være et element i den samme ringen.

EIENDOM 1. Verdien av determinanten vil ikke endres hvis alle radene i den erstattes av kolonner, og hver rad erstattes av en kolonne med samme nummer, dvs.

EIENDOM 2. Å omorganisere to kolonner eller to rader av en determinant tilsvarer å multiplisere den med -1.

EIENDOM 3. Hvis determinanten har to like kolonner eller to like rader, er den lik null.

EIENDOM 4. Å multiplisere alle elementene i en kolonne eller en rad i en determinant med et hvilket som helst tall k tilsvarer å multiplisere determinanten med dette tallet k.

EIENDOM 5. Hvis alle elementene i en kolonne eller en rad er lik null, er selve determinanten lik null. Denne egenskapen er et spesialtilfelle av den forrige (for k=0).

EIENDOM 6. Hvis de tilsvarende elementene i to kolonner eller to rader i en determinant er proporsjonale, er determinanten lik null.

EIENDOM 7. Hvis hvert element i den n'te kolonnen eller n'te rad i determinanten er summen av to ledd, kan determinanten representeres som summen av to determinanter, hvorav en i henholdsvis n'te kolonne eller i n'te. rad har den første av de nevnte termene, og den andre - den andre; elementene som står på de resterende stedene er de samme for milepælene til de tre determinantene.

EIENDOM 8. Hvis vi til elementene i en bestemt kolonne (eller en rad) legger til de tilsvarende elementene i en annen kolonne (eller en annen rad), multiplisert med en felles faktor, vil ikke verdien av determinanten endres. For eksempel. Ytterligere egenskaper til determinanter er relatert til begrepet algebraisk komplement og moll. Minor av et element er en determinant hentet fra et gitt element ved å krysse ut raden og kolonnen i skjæringspunktet for dette elementet.

Det algebraiske komplementet til ethvert element av determinanten er lik minor av dette elementet, tatt med fortegnet hvis summen av tallene i raden og kolonnen i skjæringspunktet som elementet er plassert er et partall, og med motsatt fortegn hvis dette tallet er oddetall.

Vi vil betegne det algebraiske komplementet til et element med en stor bokstav med samme navn og samme tall som bokstaven som betegner selve elementet.

EIENDOM 9. Determinanten er lik summen av produktene til elementene i en hvilken som helst kolonne (eller rad) ved deres algebraiske komplementer. Med andre ord gjelder følgende likheter:

Beregning av determinanter.

Beregningen av determinanter er basert på deres kjente egenskaper, som gjelder determinanter for alle ordener. Dette er egenskapene:

1. Hvis du omorganiserer to rader (eller to kolonner) av determinanten, vil determinanten endre fortegn.

2. Hvis de tilsvarende elementene i to kolonner (eller to rader) av determinanten er like eller proporsjonale, er determinanten lik null.

3. Verdien av determinanten vil ikke endres hvis du bytter rader og kolonner, og opprettholder rekkefølgen.

4. Hvis alle elementene i en rad (eller kolonne) har en felles faktor, kan den tas ut av determinanttegnet.

5. Verdien av determinanten vil ikke endres hvis de tilsvarende elementene i en annen rad (eller kolonne) legges til elementene i en rad (eller kolonne), multiplisert med samme tall. For tredjeordens determinanter kan denne egenskapen skrives for eksempel slik:

6. Andreordens determinanten beregnes ved hjelp av formelen

7. Den tredje ordens determinant beregnes ved hjelp av formelen

Det er et praktisk skjema for å beregne tredjeordens determinanten (se fig. 1 og fig. 2).

I henhold til diagrammet vist i fig. 1, er produktene av tilkoblede elementer tatt med sitt eget tegn, og i henhold til diagrammet i fig. 2 - med revers. Verdien av determinanten er lik den algebraiske summen av de resulterende seks produktene.

Systemer av lineære ligninger. Grunnleggende begreper og definisjoner.

Systemmр lineære algebraiske ligninger Medn ukjent(eller, lineært system, også brukt forkortelse SLAU) V lineær algebra er et likningssystem av formen

System lineære ligninger fra tre variabler bestemmer settet fly. Skjæringspunktet er løsningen.

Her er antall ligninger, og er antall ukjente. x 1 , x 2 , …, x n- ukjente som må fastslås. en 11 , en 12 , …, en mn- systemkoeffisienter - og b 1 , b 2 , … b m- gratis medlemmer - antas å være kjent . Koeffisientindekser ( en ij) systemer angir ligningstall ( Jeg) og ukjent ( j), hvor denne koeffisienten står, henholdsvis .

System (1) kalles homogen , hvis alle dens frie termer er lik null ( b 1 = b 2 = … = b m= 0), ellers - heterogen.

System (1) kalles torget , hvis nummer m ligninger lik tallet n ukjent.

Løsning systemer (1) - sett n tall c 1 , c 2 , …, c n, slik at substitusjon av hver c Jeg i stedet for x Jeg inn i system (1) gjør alle ligningene til identiteter.

System (1) kalles ledd , hvis den har minst én løsning, og ikke-ledd, hvis hun ikke har en eneste løsning.

Et fellessystem av type (1) kan ha en eller flere løsninger.

Løsninger c 1 (1) , c 2 (1) , …, c n(1) og c 1 (2) , c 2 (2) , …, c n(2) fellessystemer av formen (1) kalles diverse, hvis minst en av likestillingene brytes:

c 1 (1) = c 1 (2) , c 2 (1) = c 2 (2) , …, c n (1) = c n (2) .

Et felles system av formen (1) kalles sikker , hvis den har en unik løsning; hvis den har minst to forskjellige løsninger, kalles den usikker. Hvis det er flere ligninger enn ukjente, kalles det omdefinert .

Metoder for å løse systemer av lineære ligninger (Cramer og Gauss metode).

Gauss metode - klassisk løsningsmetode lineære systemer algebraiske ligninger (SLAU). Dette er metoden for sekvensiell eliminering variabler, når, ved hjelp av elementære transformasjoner, et likningssystem reduseres til et ekvivalent trekantsystem, hvorfra alle andre variabler finnes sekvensielt, og starter med de siste (etter antall) variabler .

Cramers metode (Cramers regel)- metode for å løse firkanter systemer av lineære algebraiske ligninger med ikke-null avgjørende faktor hovedmatrise(og for slike ligninger er det en unik løsning). Kalt ved navn Gabriel Kramer(1704–1752), som oppfant metoden.

Vektorer. Lineære operasjoner på dem.

En vektor er et rettet segment. Hvis begynnelsen av en vektor er ved punkt A og slutten er ved punkt B, er vektoren betegnet AB. Hvis begynnelsen og slutten av vektoren ikke er angitt, er den angitt med en liten bokstav i det latinske alfabetet a, b, c,…. BA betegner en vektor rettet motsatt av vektor AB. En vektor hvis begynnelse og slutt faller sammen kalles null og er betegnet med ō. Dens retning er usikker.

Lengden eller modulen til en vektor er avstanden mellom begynnelsen og slutten. Records |AB| og |a| angi modulene til vektorene AB og a.

Vektorer kalles kollineære hvis de er parallelle med samme linje, og koplanære hvis de er parallelle med samme plan.

To vektorer sies å være like hvis de er kollineære, har samme retning og er like lange.

Lineære operasjoner på vektorer inkluderer:

1) multiplikasjon av en vektor med et tall (Produktet av en vektor a og et tall α er en vektor betegnet α∙a. (eller omvendt a∙α), hvis modul er lik |α a| =| α||a|, og retningen faller sammen med retningen til vektoren a, hvis α>0, og motsatt hvis α< 0.

2) addisjon av vektorer (Summen av vektorer er en vektor, betegnet med , hvis begynnelse er i begynnelsen av den første vektoren a 1, og slutten er på slutten av den siste vektoren a n, en brutt linje bygd opp av en sekvens av summer av vektorer. Denne addisjonsregelen kalles lukkeregelen for den stiplede linjen. I tilfellet er summen av to vektorer ekvivalent med parallellogramregelen.

Den rette linjen e med en retning gitt på den, tatt som positiv, kalles e-aksen.

En lineær kombinasjon av vektorer a i er en vektor a, definert av formelen , hvor er noen tall.

Hvis for et system med n vektorer a i likheten

er sant bare hvis dette systemet sies å være lineært uavhengig. Hvis likhet (1) er oppfylt for , hvorav minst én er forskjellig fra null, kalles systemet av vektorer ai lineært avhengig. For eksempel er alle kollineære vektorer, tre koplanare vektorer, fire eller flere vektorer i tredimensjonalt rom alltid lineært avhengige.

Tre ordnede lineært uavhengige vektorer ē 1, ē 2, ē 3 i rommet kalles basis. En ordnet trippel av ikke-koplanare vektorer danner alltid et grunnlag. Enhver vektor a i rommet kan utvides i henhold til grunnlaget ē 1, ē 2, ē 3, dvs. representerer a som en lineær kombinasjon av basisvektorer: a= xē 1 + yē 2 + zē 3, hvor x, y, z er koordinatvektoren a i grunnlaget ē 1, ē 2, ē 3. En basis kalles ortonormal hvis vektorene er gjensidig vinkelrette og har lengdeenhet. Et slikt grunnlag er betegnet med i, j, k, dvs. i=(1, 0, 0), j=(0, 1, 0), k=(0, 0, 1).

Eksempel 5. Vektorer er spesifisert i en ortonormal basis i, j, k ved koordinater: a=(2;-1;8), e 1 = (1,2,3), e 2 = (1,-1,- 2), e3 = (1,-6,0). Pass på at trippelen e 1, e 2, e 3 danner et grunnlag, og finn koordinatene til vektoren i dette grunnlaget.

Løsning. Hvis determinanten , sammensatt av koordinatene til vektorene e 1, e 2, e 3, ikke er lik 0, da er vektorene e 1, e 2, e 3 lineært uavhengige og danner derfor en basis. Vi sørger for at = -18-4+3-12=-31 Dermed er trippelen e 1, e 2, e 3 grunnlaget.

La oss betegne koordinatene til vektor a i basisen e 1 , e 2 , e 3 ved x, y, z. Da er a = (x,y,z) = xe 1 + yе 2 + zе 3. Siden ved betingelse a = 2i – j +8k, e 1 = i +2j +3k, e 2 = i – j -2k, e 3 = i – 6j, så fra likheten a = xe1 + ye 2 + zе 3 det følger at 2i – j +8k = xi + 2xj + 3xk + yi – yj -2yk +zi -6zj = (x+y+z)i +(2x-y-6z)j +(3x-2y)k. Som du kan se, er vektoren på venstre side av den resulterende likheten lik vektoren på høyre side, og dette er bare mulig hvis deres tilsvarende koordinater er like. Herfra får vi et system for å finne de ukjente x, y, z:

Dens løsning: x = 2, y = -1, z = 1. Så, a = 2e 1 – e 2 + e 3 = (2,-1,1).

Vektor nedbrytning. Punktprodukt av vektorer.

Skalært produkt Noen ganger indre produkt- operasjon på to vektorer, hvis resultat er tallet ( skalar), uavhengig av koordinatsystemet og karakteriserer lengdene til faktorvektorene og vinkelen mellom dem. Denne operasjonen tilsvarer multiplikasjon lengde vektor x på projeksjon vektor y til vektor x. Denne operasjonen anses vanligvis som kommutativ Og lineær for hver faktor.

Vanligvis brukes en av følgende notasjoner:

eller ( betegnelse Dirac, ofte brukt i kvantemekanikk for tilstandsvektorer):

Det antas vanligvis at skalarproduktet er positivt bestemt, altså

For alle .

Hvis dette ikke er forutsatt, kalles arbeidet ubestemt.

Prikk produkt V vektorrom ovenfor felt kompleks(eller ekte) tall er en funksjon for elementer som tar verdier i (eller) definert for hvert par av elementer og som tilfredsstiller følgende betingelser:

Merk at av paragraf 2 i definisjonen følger det at . Derfor gir punkt 3 mening, til tross for de komplekse (i det generelle tilfellet) verdiene prikkprodukt.

Kryssprodukt av vektorer.

Vektor kunstverk- Dette pseudovektor, vinkelrett plan konstruert fra to faktorer, som er resultatet binær operasjon"vektor multiplikasjon" over vektorer i tre dimensjoner Euklidisk rom. Arbeidet er verken kommutativ, ingen assosiativ(Det er antikommutativ) og skiller seg fra skalært produkt av vektorer. I mange ingeniør- og fysikkproblemer må du kunne konstruere en vektor vinkelrett på to eksisterende - vektorproduktet gir denne muligheten. Kryssproduktet er nyttig for å "måle" vinkelrettheten til vektorer - lengden på kryssproduktet til to vektorer er lik produktet av lengdene deres hvis de er vinkelrette, og avtar til null hvis vektorene er parallelle eller antiparallelle.

Vektorproduktet kan defineres på forskjellige måter, og teoretisk, i et rom av enhver dimensjon n du kan beregne produktet n-1 vektorer, oppnå en enkelt vektor vinkelrett på dem alle. Men hvis produktet er begrenset til ikke-trivielle binære produkter med vektorresultater, er det tradisjonelle vektorproduktet bare definert i tre dimensjoner og sjudimensjonal mellomrom. Resultat vektor produkt, som skalaren, avhenger av beregninger Euklidisk rom.

I motsetning til formelen for beregning fra vektorkoordinater prikkprodukt i tre dimensjoner rektangulært koordinatsystem, formelen for kryssproduktet avhenger av orientering rektangulært koordinatsystem eller, med andre ord, dets " kiralitet».

Blandet produkt av vektorer

Blandet produkt vektorer - skalært produkt vektor på vektor produkt vektorer Og:

Noen ganger kalles det trippelskalært produkt vektorer, tilsynelatende på grunn av at resultatet er skalar(mer presist - pseudoskalær).

Geometrisk betydning: Modulen til det blandede produktet er numerisk lik volumet parallellepipedum, utdannet vektorer .

Blandet stykke skjev-symmetrisk i forhold til alle dens argumenter:

det vil si at omorganisering av to faktorer endrer produktets fortegn. Det følger at

Spesielt,

Et blandet verk kan enkelt skrives ved hjelp av Levi-Civita symbol (tensor):

(i den siste formelen på ortonormal basis kan alle indekser skrives som lavere; i dette tilfellet gjentar denne formelen formelen helt direkte med determinanten, men i dette tilfellet oppnås en multiplikator (-1) automatisk for venstre baser).

Kartesisk rektangulært koordinatsystem på et plan.

La oss ta to innbyrdes vinkelrette rette linjer på planet - to koordinatakser Ox og Oy med de positive retningene angitt på dem (fig. 1). De rette linjene Ox og Oy kalles koordinatakser, punktet for deres skjæringspunkt O er opprinnelsen til koordinatene.

Koordinataksene Ox, Oy med den valgte målestokkenheten kalles et kartesisk rektangulært (eller rektangulært) koordinatsystem på planet.

La oss tilordne to tall til et vilkårlig punkt M i planet: abscissen x, lik avstanden fra punktet M til Oy-aksen, tatt med "+"-tegnet hvis M ligger til høyre for Oy, og med "-" tegn hvis M ligger til venstre for Oy; y-ordinaten, lik avstanden fra punkt M til Ox-aksen, tatt med "+"-tegnet hvis M ligger over Ox, og med "-"-tegnet hvis M ligger under Ox. Abscissen x og ordinaten y kalles de kartesiske rektangulære koordinatene til punktet M(x;y).

Opprinnelsen har koordinater (0;0). Koordinatakser deler planet i fire deler som kalles kvartaler eller kvadranter (noen ganger også kalt koordinatvinkler). Den delen av planet som er innelukket mellom de positive halvaksene Ox og Oy kalles den første kvadranten. Deretter nummereres kvadrantene mot klokken (fig. 2). For alle punkter i første kvadrant x>0, y>0; for punkt I i kvadrant x<0, у>0, i I I I kvadrant x<0, у<0 и в IV квадранте х>0, y<0.

Polare koordinater.

Polar koordinatsystem- et todimensjonalt koordinatsystem der hvert punkt på planet er definert av to tall - den polare vinkelen og den polare radiusen. Det polare koordinatsystemet er spesielt nyttig i tilfeller der forhold mellom punkter er lettere representert i form av radier og vinkler; i de mer vanlige kartesisk eller rektangulært koordinatsystem, kan slike relasjoner bare etableres ved å søke trigonometrisk ligninger.

Det polare koordinatsystemet er definert av en stråle, som kalles null- eller polaraksen. Punktet der denne strålen kommer ut kalles opprinnelsen eller polen. Ethvert punkt på planet er definert av to polare koordinater: radial og vinkel. Den radielle koordinaten (vanligvis betegnet med ) tilsvarer avstanden fra et punkt til origo. Vinkelkoordinat, også kalt polarvinkel eller asimut og er betegnet , er lik vinkelen som polaraksen må roteres mot klokken for å komme til dette punktet.

Den radielle koordinaten definert på denne måten kan ta verdier fra null før evighet, og vinkelkoordinaten varierer fra 0° til 360°. For enkelhets skyld kan imidlertid verdiområdet til polarkoordinatene utvides utover

Ligning av en rett linje på et plan

Definisjon. Enhver rett linje på planet kan spesifiseres med en førsteordens ligning

Axe + Wu + C = 0,

Dessuten er konstantene A og B ikke lik null på samme tid. Denne førsteordensligningen kalles generell ligning av en rett linje. Avhengig av verdiene til konstantene A, B og C, er følgende spesielle tilfeller mulig:

C = 0, A ≠0, B ≠ 0 – den rette linjen går gjennom origo

A = 0, B ≠0, C ≠0 (By + C = 0) - rett linje parallelt med okseaksen

B = 0, A ≠0, C ≠ 0 (Ax + C = 0) – rett linje parallelt med Oy-aksen

B = C = 0, A ≠0 – den rette linjen faller sammen med Oy-aksen

A = C = 0, B ≠0 – den rette linjen faller sammen med okseaksen

Ligningen til en rett linje kan presenteres i forskjellige former avhengig av gitte startbetingelser.

Hovedoppgavene med å bruke ligningen til en linje

Kan ikke svare

Andre ordens kurver

Andre ordens kurve- geometrisk lokus av punkter hvis kartesiske rektangulære koordinater tilfredsstiller en ligning av formen

der minst én av koeffisientene er forskjellig fra null.

Begrensning av tallrekkefølge og funksjon

Begrensning av nummersekvens. Tenk på en tallsekvens hvis vanlige term nærmer seg et tall en øke serienummeret n. I dette tilfellet sies tallsekvensen å ha grense. Dette konseptet har en strengere definisjon.

Denne definisjonen betyr det en Det er grense tallsekvens hvis den vanlige termen nærmer seg uten grense en med økende n. Geometrisk betyr dette at for enhver > 0 kan man finne et slikt tall N som starter fra n > N alle medlemmer av sekvensen er plassert innenfor intervallet ( en en). En sekvens som har en grense kalles konvergent; ellers - avvikende.

Sekvensen kalles begrenset, hvis et slikt tall eksisterer M hva | u n | M  for alle n . En økende eller minkende sekvens kalles monotont.

Grunnleggende teoremer om grenser og deres anvendelser

Teorem 1 . (om overgang til grensen i likhet) Hvis to funksjoner har samme verdier i nærheten av et bestemt punkt, faller grensene deres på dette tidspunktet sammen.

Teorem 2. (om overgang til grensen i ulikhet) Hvis funksjonen verdier f(x) i nærheten av et bestemt punkt ikke overskride de tilsvarende verdiene til funksjonen g(x) , deretter grensen for funksjonen f(x) på dette tidspunktet ikke overskrider grensen for funksjonen g(x) .

Teorem 3 . Grensen for en konstant er lik konstanten selv.

Bevis. f(x)=c, la oss bevise det .

La oss ta en vilkårlig >0. Som  kan du ta hvilken som helst

positivt tall. Så kl

Teorem 4. Funksjon kan ikke ha to forskjellige grenser

Et poeng.

Bevis. La oss anta det motsatte. La

Og .

Av teoremet om sammenhengen mellom grensen og den infinitesimale funksjonen:

f(x)- EN= - b.m. kl ,

f(x)- B= - b.m. kl.

Ved å trekke fra disse likhetene får vi:

B-EN= - .

Ved å gå til grensene på begge sider av likestillingen på , har vi:

B-EN=0, dvs. B=EN. Vi får en selvmotsigelse som beviser teoremet.

Teorem 5. Hvis hvert ledd i en algebraisk sum av funksjoner har en grense ved , så har den algebraiske summen også en grense ved , og grensen for den algebraiske summen er lik den algebraiske summen av grensene.

.

Bevis. La , , .

Så, ved teorem om sammenhengen mellom grensen og b.m. funksjoner:

Hvor - b.m. kl.

La oss legge til disse likhetene algebraisk:

f(x)+ g(x)- h(x)-(A+B-C)= ,

Hvor b.m. kl.

I følge teoremet om sammenhengen mellom grensen og b.m. Egenskaper:

A+B-C= .

Teorem 6. Hvis hver av faktorene til et produkt av et begrenset antall funksjoner har en grense ved , så har produktet også en grense ved , og grensen for produktet er lik produktet av grensene.

.

Konsekvens. Konstantfaktoren kan tas utover grensetegnet.

.

Teorem 7. Hvis funksjonene f(x) Og g(x) har en grense på ,

og , så har deres kvotient også en grense ved , og grensen for kvotienten er lik kvotienten til grensene.

, .

Kontinuitet i funksjon

I fig. 15, og grafen for funksjonen vises . Det er naturlig å kalle det en kontinuerlig graf fordi den kan tegnes med én bevegelse av en blyant uten å løfte den fra papiret. La oss sette et vilkårlig punkt (tall). Et annet punkt i nærheten av det kan skrives i formen , der det er et positivt eller negativt tall kalt inkrement. Forskjell

kalles inkrementet til funksjonen i punktet som tilsvarer inkrementet. Det som menes her er det . I fig. 15, og er lik lengden på segmentet.

Vi vil strebe mot null; så for den aktuelle funksjonen vil den åpenbart ha en tendens til null:

. (1)

La oss nå se på grafen i fig. 15, b. Den består av to sammenhengende deler og. Disse brikkene henger imidlertid ikke kontinuerlig sammen, og derfor er det naturlig å kalle grafen for diskontinuerlig. For at grafen skal vise en funksjon med én verdi ved punktet , la oss bli enige om at den er lik lengden på segmentet som forbinder og ; som et tegn på dette er punktet avbildet på grafen med en sirkel, mens punktet har en pil tegnet som indikerer at det ikke tilhører grafen. Hvis punktet tilhørte grafen, ville funksjonen vært toverdi ved punktet.

La oss nå legge til et inkrement og bestemme den tilsvarende økningen av funksjonen:

Hvis vi har en tendens til null, kan vi nå ikke lenger si hva som vil ha en tendens til null. For negative som har en tendens til null, er dette sant, men for positive er dette ikke i det hele tatt: fra figuren er det klart at hvis, mens de forblir positive, har en tendens til null, så tenderer den tilsvarende økningen til et positivt tall som er lik til lengden av segmentet.

Etter disse betraktningene er det naturlig å kalle en funksjon definert på et intervall kontinuerlig i et punkt på dette segmentet hvis inkrementet på dette punktet, som tilsvarer inkrementet, har en tendens til null på noen måte som det har en tendens til null. Dette (egenskapen til kontinuitet i) er skrevet i form av relasjon (1) eller også slik:

Oppføring (2) lyder slik: grensen er lik null når den har en tendens til null i henhold til enhver lov. Imidlertid er uttrykket "i henhold til enhver lov" vanligvis utelatt, noe som antyder det.

Hvis en funksjon definert på ikke er kontinuerlig ved punktet , det vil si hvis egenskap (2) ikke holder for den på minst én måte å vende mot null, kalles den diskontinuerlig i punktet .

Funksjonen vist i fig. 15, a, er kontinuerlig på ethvert punkt, men funksjonen vist i fig. 15, b, åpenbart, er kontinuerlig på ethvert punkt, med unntak av punktet, fordi for sistnevnte, forhold (2) er ikke tilfredsstilt når, forblir positiv.

En funksjon som er kontinuerlig på et hvilket som helst punkt på et segment (intervall) kalles kontinuerlig på det segmentet (intervall).

En kontinuerlig funksjon uttrykker matematisk en egenskap som vi ofte møter i praksis, nemlig at et lite inkrement i en uavhengig variabel tilsvarer et lite inkrement i en avhengig variabel (funksjon). Utmerkede eksempler på en kontinuerlig funksjon er ulike bevegelseslover for kropper, som uttrykker avhengigheten av banen som kroppen har reist i tide. Tid og rom er kontinuerlige. Denne eller den bevegelsesloven etablerer en viss kontinuerlig forbindelse mellom dem, preget av det faktum at en liten økning av tiden tilsvarer en liten økning av banen.

Mennesket kom til abstraksjonen av kontinuitet ved å observere de såkalte kontinuerlige mediene rundt seg - fast, flytende eller gassformig, for eksempel metaller, vann, luft. Faktisk er ethvert fysisk medium en akkumulering av et stort antall bevegelige partikler skilt fra hverandre. Imidlertid er disse partiklene og avstandene mellom dem så små sammenlignet med volumene av medier som man må forholde seg til i makroskopiske fysiske fenomener at mange slike fenomener kan studeres ganske godt hvis vi vurderer omtrentlig massen til mediet som studeres for å være kontinuerlig distribuert uten hull i plassen som den opptar. Mange fysiske disipliner er basert på denne antakelsen, for eksempel hydrodynamikk, aerodynamikk og elastisitetsteori. Det matematiske kontinuitetsbegrepet spiller naturlig nok en stor rolle i disse disiplinene, som i mange andre.

Kontinuerlige funksjoner utgjør hovedklassen av funksjoner som matematisk analyse opererer med.

Eksempler på kontinuerlige funksjoner er elementære funksjoner (se § 3.8 nedenfor). De er kontinuerlige over endringsintervallene der de er definert.

Diskontinuerlige funksjoner i matematikk reflekterer diskontinuerlige prosesser som finnes i naturen. Under et sammenstøt endres for eksempel hastigheten til en kropp brått. Mange kvalitetsoverganger er ledsaget av hopp. For eksempel, forholdet mellom temperaturen på ett gram vann (is) og mengden kalorier av varme som finnes i den, når den endres mellom og , hvis vi konvensjonelt antar at ved verdien av , uttrykkes ved følgende formler:

Vi antar at varmekapasiteten til is er 0,5. Når denne funksjonen viser seg å være ubestemt – med flere verdier; For enkelhets skyld kan vi være enige om at det tar en veldig bestemt verdi, for eksempel . Funksjonen, åpenbart diskontinuerlig ved , er vist i fig. 16.

La oss definere kontinuiteten til en funksjon ved et punkt.

En funksjon kalles kontinuerlig ved et punkt hvis den er definert i et eller annet nabolag til dette punktet, inkludert ved selve punktet, og hvis økningen på dette punktet, tilsvarende økningen av argumentet, har en tendens til null ved:

Hvis vi setter , får vi følgende ekvivalente definisjon av kontinuitet ved: en funksjon er kontinuerlig i et punkt hvis den er definert i et eller annet nabolag til dette punktet, inkludert ved selve punktet, og hvis

; (4)

eller også på språket: hvis det for alle er slikt at

Likhet (4) kan også skrives som følger:

. (4’)

Den viser at man under tegnet av en kontinuerlig funksjon kan gå til grensen.

Eksempel 1. En konstant er en funksjon som er kontinuerlig til enhver tid. Faktisk tilsvarer et punkt verdien av en funksjon, et punkt tilsvarer den samme verdien . Derfor

.

EKSEMPEL 2. Funksjonen er kontinuerlig for enhver verdi fordi og derfor for .

Eksempel 3. Funksjonen er kontinuerlig for enhver . Faktisk,

Men for alle er det ulikhet

Hvis , så følger dette av fig. 17, som viser en sirkel med radius 1 (lengdebuen er større enn korden dekket av den, som har lengde ). Når ulikhet (6) blir til likhet. Hvis da . Til slutt, hvis, da . Fra (5) basert på (6) følger det

,

Men så åpenbart

Vi kan også si at for alle er det mulig å finne akkurat slikt

La oss merke oss et viktig teorem.

Teorem 1. Hvis funksjoner og er kontinuerlige i et punkt, så er deres sum, differanse, produkt og kvotient (at) også kontinuerlige på dette punktet.

Denne teoremet følger direkte av teorem 6 §3.2, tatt i betraktning at i dette tilfellet

Et viktig teorem om kontinuiteten til en funksjon fra en funksjon (kompleks funksjon) er også sant.

Teorem 2. La en funksjon gis som er kontinuerlig i punktet , og en annen funksjon som er kontinuerlig i punktet , og la . Deretter den komplekse funksjonen er kontinuerlig på punktet.

Bevis. Merk at ved definisjonen av kontinuitet til en funksjon på et punkt følger det at den er definert i et eller annet nabolag til dette punktet. Derfor

Her innføres en substitusjon og det tas hensyn til kontinuitet på punktet .

Eksempel 4. Funksjon

hvor er konstante koeffisienter, kalles et gradspolynom. Det er kontinuerlig for alle. Tross alt, for å oppnå, er det nødvendig, basert på konstante tall og funksjonen, å utføre et endelig antall aritmetiske operasjoner - addisjon, subtraksjon og multiplikasjon. Men en konstant er en kontinuerlig funksjon (se eksempel 1), og en funksjon er også kontinuerlig (se eksempel 2), så kontinuitet følger av teorem 1.

Eksempel 5. Funksjonen er kontinuerlig. Det er en sammensetning av to kontinuerlige funksjoner: , .

Eksempel 6. Funksjon

er kontinuerlig for den spesifiserte , fordi (se setning 1) den er lik kvotienten av delingen av kontinuerlige funksjoner og divisoren er ikke lik null (for den spesifiserte ).

Eksempel 7. Funksjon

er kontinuerlig for enhver , fordi det er en sammensetning av kontinuerlige funksjoner: , , (se setning 2).

Eksempel 8. Funksjonen er kontinuerlig pga

Eksempel 9. Hvis en funksjon er kontinuerlig på et punkt, så er funksjonen også kontinuerlig på dette punktet.

Dette følger av setning 2 og eksempel 8, fordi en funksjon er en sammensetning av to sammenhengende funksjoner, .

La oss merke oss ytterligere to teoremer som følger direkte av de tilsvarende teoremene 1 og 2 i §3.2 for grensen til en funksjon.

Teorem 3. Hvis en funksjon er kontinuerlig i et punkt, så er det et nabolag til dette punktet der den er avgrenset.

Teorem 4. Hvis funksjonen er kontinuerlig ved punktet og , så er det et nabolag til punktet der

.

Dessuten, hvis , da

og hvis, da

Konseptet med derivat.

Derivat(fungerer på et punkt) - grunnleggende konsept differensialregning, som karakteriserer endringshastigheten til funksjonen (på et gitt punkt). Definert som grense forholdet mellom inkrementet til en funksjon og dets inkrement argument når argumentøkningen har en tendens til null, hvis en slik grense eksisterer. En funksjon som har en endelig derivert (på et tidspunkt) kalles differensierbar (på det tidspunktet).

Prosessen med å beregne den deriverte kalles differensiering. Omvendt prosess - å finne antiderivat - integrering.

Geometrisk og mekanisk betydning av derivater..

Regler for differensiering.

Derivert av en algebraisk sum av funksjoner

Teorem 1. Derivat summen (forskjellen) av to differensierbare funksjoner er lik summen (forskjellen) av de deriverte av disse funksjonene:

(u±v)" = u"±v"

Konsekvens. Den deriverte av en endelig algebraisk sum av differensierbare funksjoner er lik den samme algebraiske summen av deriverte av ledd. For eksempel,

(u - v + w)" = u" - v" + w"

Den deriverte av produktet av funksjoner bestemmes av

Teorem 2. Den deriverte av produktet av to differensierbare funksjoner er lik produktet av den første funksjonen og den deriverte av den andre pluss produktet av den andre funksjonen og den deriverte av den første, dvs.

(uv)" = u"v + uv"

Konsekvens 1. Konstantfaktoren kan tas ut av tegnet til den deriverte (cv)" = cv" (c = const).

Konsekvens 2. Den deriverte av produktet av flere differensierbare funksjoner er lik summen av produktene av den deriverte av hver av dem med alle de andre.

For eksempel, (uvw)" = u"vw + uv"w + uvw"

Derivert av kvotienten til to funksjoner

er uttrykt ved følgende teorem.

Teorem 3. Den deriverte av kvotienten til to differensierbare funksjoner bestemmes av formelen

Den deriverte av en kompleks funksjon uttrykkes ved

Teorem 4. Hvis y = f(u) og u = (ф(x)) er differensierbare funksjoner av deres argumenter, så avledet av en kompleks funksjon y = f (ф(x)) eksisterer og er lik produktet av den deriverte av denne funksjonen med hensyn til det mellomliggende argumentet og den deriverte av det mellomliggende argumentet med hensyn til den uavhengige variabelen, dvs.

Veldig ofte i prøver i matematikk på derivater komplekse funksjoner er gitt, for eksempel y = sin(cos5x). Den deriverte av en slik funksjon er lik -5sin5x*sin(cos5x)

Se et eksempel på beregning av en kompleks funksjon i følgende video

Derivater av elementære funksjoner.

Derivater av elementære funksjoner til et enkelt argument	Funksjony = f (kx +b )	Derivater av elementære funksjoner til et komplekst argument
y=xn	y=nxn−1	y=(kx+b)n	y=nk(kx+b)n−1
		y=(kx+b)

sjoner, på grunn av hvilke likestilling (3.10) spiller en viktig rolle både i teoretiske studier og i omtrentlige beregninger.

Operasjonene for å finne den deriverte og differensialen til en funksjon kalles differensiering denne funksjonen. Vanlig navn begge operasjonene forklares med deres åpenbare avhengighet. I kraft av formel (3.8) oppnås funksjonens differensial enkel multiplikasjon sin produksjon

bærerfeil som oppstår når du erstatter inkrementet til en funksjon med dens differensial.

La oss finne inkrementet og differensialet til funksjonen

y = 3(x+ x) 2 + (x+ x) − 3 x2 − x= 6 x x+ 3(x) 2 + x= (6 x+ 1) x+ (x) 2 .

Så dy = (6 x + 1) x. La oss beregne udy ved punktet x = 1 hvis x = 0, 1 y = 7 0, 1 + 3 0, 01 = 0, 73; dy = 7 0, 1 = 0, 7.

Den absolutte feilen er y − dy = 0,73 − 0,7 = 0,03, og den relative feilen

y = 0 0, , 03 73 ≈0,04.

3.5. Derivert av sum, produkt og kvotient av funksjoner

La oss huske de kjente fra kurset videregående skole differensieringsregler, som tillater i noen tilfeller å finne avledede funksjoner uten direkte å ty til definisjon.

Teorem 3.3. Hvis funksjonene u = u (x) og v = v (x)

ved punkt x, deretter på dette punktet
				(u+v)
				(uv)		U v+ v u;
					u v − v u				V = v (x) ≠ 0.

differensierbar

Ved å multiplisere disse likhetsleddene med dx, får vi de samme reglene skrevet i form av differensialer

d (u+ v) = du+ dv;
d (uv) = udv+ vdu;

					udv − vdu

Bevis. Siden beviset for alle deler av teoremet utføres helt jevnt, vil vi bevise en av dem, for eksempel den andre.

La oss betegne y = uv. La oss gi x øke x , og la

u , Δ v , Δ y vil være inkrementene til funksjonene u , v , y ved punktet									x , tilsvarende-
øke		x , argument. Deretter
y = (u+ u)(v+ v) − uv= v u+ u v+ u v.
Med tanke på at u	og v er verdiene til funksjonene i punktet							x er ikke avhengig av
argumentrotasjoner		x , på grunn av definisjon (3.1) og egenskapene til grensen
overgang (se formler (2.14), (2.15) finner vi
y ′ =lim		Vlim		Ulim	v+lim
x→ 0		x→ 0		x→ 0		x→ 0		x→ 0
Funksjon v = v(x)	på det aktuelle punktet					x i henhold til betingelsene for differensialsetningen

refererbar, og derfor kontinuerlig (setning 3.2), derfor

	v = 0 (kontinuitetsdefinisjon 2.17) og forrige likhet
x→ 0					y ′ = vu ′+ uv ′+ u 0 . Erstatter her
gir et uttrykk for den deriverte:
y = uv , vi kommer til formel (3.12).							y = C (her
	Derivert og differensial av en konstant funksjon
MED -	konstant tall for alle x X )					er lik null.
	x X C
					dC = C dx= 0 .
Faktisk, på alle punkter i settet X har en slik funksjon en
og samme betydning, på grunn av det for henne						y ≡ 0 for noen	x av disse
	x , x + x X . Herfra,			på grunn av definisjonen av derivat og differensial
regional, formler (3.17) følger.
	Formel (3.11) er generalisert til tilfellet med et begrenset antall svake
nødvendige funksjoner.
	Når u = C, hvor	C − const, formler (3.12) og (3.15),					på grunn av (3.17),
				d(Cv) = Cdv. Det vil si den konstante multi-
gi likheter: (Cv)

Tel kan tas ut av deriverte og differensialtegn.

For tre faktorer, suksessivt bruk av formelen

(3.12), finner vi

(uvw) ′ = ((uv) w) ′ = (uv) ′ w+ (uv) w′+ (u′ v+ uv′ ) w+ uvw′ = = u ′ vw + uv ′ w + uvw .

En lignende regel er gyldig når man differensierer produktet av en rekke faktorer.

I de følgende avsnittene vil derivater av de viktigste elementære funksjonene bli oppnådd.

3.6. Derivater av trigonometriske funksjoner

La oss finne de deriverte av trigonometriske funksjoner, nemlig

		Cosx						= − sinx
	(synd x)					(cos x)
	(tgx) ′ =					(ctgx)′
			cos2 x						synd2 x

La oss ta den første. Inkrement av funksjon y = sin x ved punktx, co-

	tilsvarende økning				argument, vil det være
	y = sin(x+		x )− sinx = 2sin				x cos(x +		x) .
	Tatt i betraktning at synd 2 x		2 x kl
						x → 0	og bruke definisjonen av produksjon
	vann, finner vi				2sin 2 x cos(x +			2x)
	y ′ =lim		y = lim
		x→ 0		x→ 0
		2 2 x cos(x +		2x)		Limcos(x +		x )= cosx .
	x→ 0					x→ 0

Den andre formelen er bevist på lignende måte. Den tredje og fjerde formelen oppnås hvis tangens og cotangens er uttrykt i form av sinus og cosinus og bruker formel (3.13).

3.7. Differensiere logaritmiske funksjoner

	Formlene holder
					loga e
		(logg x)				2. (lnx)

La oss bevise den første av dem. Inkrement av funksjon y = log a x ved punktx, co-

tilsvarende økningen x		argument, vil det være
y = loga (x + x )− loga x = loga		x + x	Loga (1+	x )= loga e ln(1+	x) ;

(vi brukte her identitetsloggen a A = log a e ln A ).

Siden ln(1 + x x ) x x		x → 0		Deretter, per definisjon, derivat
vi får:	y = log e lim								x )=
y ′ =lim							ln(1+
x→ 0			x→ 0
Loga e lim								loga e.
	x→ 0

3.8. Differensiering av en kompleks funksjon.

Derivater av potens og eksponentielle funksjoner

La en kompleks funksjon y argumenterx gis av formlene y = f (u),

u = ϕ (x) (se avsnitt 1.4.3)

Teorem 3.4 (om den deriverte av en kompleks funksjon). Hvis funksjonene

y = f (u), u = ϕ (x) er differensierbare		i det aktuelle	hverandre
punktene u og x, deretter den komplekse funksjonen		f [ϕ(x)] er også differensierbar i
	x, og	y ′x = y ′u u ′x .
	y ′ =f ′(u ) u ′or
Bevis. Vi vil gi en økning til den uavhengige variabelen x
	x, da vil funksjonen u = ϕ (x) motta en økning u,		hva som vil forårsake

økning y av funksjon y = f (u) . Siden funksjonen y = f (u) i henhold til betingelsene for teoremet er differensierbar ved punktet u som vurderes, kan inkrementet på dette punktet representeres i formen (se Definisjon 3.4)

			u , hvor α (		u ) → o når u → 0 .
y = f(u) u+ α (u)
				f(u)	x + α(u)
Funksjon u = ϕ(x)			differensierbar, og derfor kontinuerlig på nøyaktig
ke x som tilsvarer punktet u vurdert ovenfor							(Setning 3.2).
Derfor,				kontinuitet		lim u = 0,	og derfor
						x→ 0
lim α (u )= 0.
x→ 0
Med tanke på dette,		overgang inn			siste	likestilling til	grense kl

x → 0, kommer vi til (3.18).

Ved å multiplisere likhetsleddet (3.18) med dx, får vi et uttrykk for differensialen til en kompleks funksjon

dy = f′ (u) du.

Kommentar. Differensialen til funksjonen y = f (u) ville ha nøyaktig samme form hvis argumentet u ikke var en funksjon, men en uavhengig variabel. Det er dette som kalles invarians egenskap(uavhengighet) av formen til differensialen med hensyn til argumentet. Det bør huskes at hvis u er en uavhengig variabel, så er du = u dens vilkårlige økning, hvis u er et mellomargument (det vil si en funksjon), så er du differensialen til denne funksjonen, det vil si en verdi som ikke sammenfaller med inkrementet u.

Ved å bruke det siste teoremet er det enkelt å få frem differensieringsformler

dannelse av makt og eksponentielle funksjoner:

α− 1

2). (en

ln a;

3). (e

1). (x

) = α x

Egentlig,

forutsatt

x > 0,

ta logaritmer fra begge sider

formler y = x α; ln y = α ln x . Her

Dette er en funksjon av x, på grunn av hvilken

venstre side av den siste likheten er en kompleks funksjon av x. Ved å differensiere begge sider av den siste likheten med hensyn til x (venstre side som en kompleks funksjon), får vi

1 y y ′ =a 1 x ,

y ′ =ay x =ax x a =ax a − 1 .

Det er lett å vise at dette resultatet også er sant for x< 0 , если только при

i dette tilfellet gir x α mening. Tidligere ble resultatet oppnådd for tilfellet α = n. Den andre formelen oppnås på samme måte, hvorfra, i det spesielle tilfellet av a = e, den siste formelen følger.

Kommentar. Teknikken med foreløpig logaritme, som ble brukt for å oppnå formelen for å differensiere en potensfunksjon, har uavhengig betydning og kalles i forbindelse med det påfølgende funnet av den deriverte av logaritmen til funksjonen

lnx ) "= cosx lnx + sin x x .

Derfor,

y ′ = x sin x (cosx lnx + sin x x)

Kommentar. Regelen for å differensiere en kompleks funksjon kan også brukes for å finne den deriverte av en funksjon spesifisert implisitt.

Faktisk, hvis forholdet mellom x og y er gitt på formen F (x, y) = 0 og denne ligningen er løsbar i forhold til y, så kan den deriverte y ′ finnes fra ligningen

					(F (x, y (x))= 0.
Eksempel 3.4.								y = f (x) gitt ikke-
		Finn den deriverte av en funksjon
eksplisitt ved ligning		arctan(y) − y+ x= 0 .				y funksjon fra x:
Vi differensierer likheten med hensyn til x, med tanke på
	y′						1 + år
			− y ′+ 1= 0, hvorfra			y′ =
	1 +y 2

3.9. Differensiering av en invers funksjon.

Differensiering av inverse trigonometriske funksjoner

La to gjensidig inverse funksjoner gis: y = f (x) og x = ϕ (y)

(se punkt 1.4.8).

Teorem 3.5 (om den deriverte av den inverse funksjonen). Hvis funksjonene

y = f(x) ,

x = ϕ (y)

øke (minske) og ved punkt x funksjonen f (x)

differensierbar

f ′ (x) ≠ 0, deretter ved det tilsvarende punktet

funksjonen ϕ (y) er også differensierbar (med hensyn til y), og

Bevis.

la oss angi inkrementet

x = ϕ (y)

øker

(minkende)

x = ϕ (y + y )− ϕ (y )≠ 0og

Under teoremets betingelser

x = ϕ (y)

x → 0

y → 0

er kontinuerlig (setning 3.2), på grunn av hvilket

Første nivå

Derivert av en funksjon. Omfattende guide (2019)

La oss forestille oss en rett vei som går gjennom et kupert område. Det vil si at den går opp og ned, men svinger ikke til høyre eller venstre. Hvis aksen er rettet horisontalt langs veien og vertikalt, vil veilinjen være veldig lik grafen til en kontinuerlig funksjon:

Aksen er et visst nivå på null høyde; i livet bruker vi havnivået som det.

Når vi beveger oss fremover langs en slik vei, beveger vi oss også opp eller ned. Vi kan også si: når argumentet endres (bevegelse langs abscisseaksen), endres verdien av funksjonen (bevegelse langs ordinataksen). La oss nå tenke på hvordan vi bestemmer "brattheten" på veien vår? Hva slags verdi kan dette være? Det er veldig enkelt: hvor mye høyden vil endre seg når du beveger deg en viss avstand fremover. Tross alt, på ulike områder veier, når vi beveger oss fremover (langs x-aksen) med én kilometer, vil vi stige eller falle med et annet antall meter i forhold til havnivået (langs y-aksen).

La oss betegne fremgang (les "delta x").

Den greske bokstaven (delta) brukes ofte som et prefiks i matematikk, som betyr "forandring". Det vil si - dette er en endring i mengde, - en endring; så hva er det? Det stemmer, en endring i størrelsesorden.

Viktig: et uttrykk er en enkelt helhet, én variabel. Aldri skille "delta" fra "x" eller noen annen bokstav! Det er for eksempel.

Så vi har gått fremover, horisontalt, ved. Hvis vi sammenligner veiens linje med grafen til funksjonen, hvordan betegner vi da stigningen? Gjerne,. Det vil si at når vi beveger oss fremover, stiger vi høyere.

Verdien er lett å beregne: hvis vi i begynnelsen var i en høyde, og etter å ha flyttet vi befant oss i en høyde, da. Hvis endepunktet er lavere enn startpunktet, vil det være negativt - dette betyr at vi ikke stiger opp, men synker.

La oss gå tilbake til "bratthet": dette er en verdi som viser hvor mye (bratt) høyden øker når du beveger deg en avstandsenhet fremover:

La oss anta at på en del av veien, når man beveger seg en kilometer fremover, stiger veien opp med en kilometer. Da er helningen på dette stedet lik. Og hvis veien, mens den beveget seg fremover med m, sank med km? Da er helningen lik.

La oss nå se på toppen av en ås. Hvis du tar begynnelsen av strekningen en halv kilometer før toppen, og slutten en halv kilometer etter den, kan du se at høyden er nesten den samme.

Det vil si, ifølge vår logikk viser det seg at helningen her er nesten lik null, noe som tydeligvis ikke stemmer. Litt over en strekning på kilometer kan mye endre seg. Det er nødvendig å vurdere mindre områder for en mer adekvat og nøyaktig vurdering av bratthet. Hvis du for eksempel måler høydeendringen når du beveger deg én meter, vil resultatet bli mye mer nøyaktig. Men selv denne nøyaktigheten er kanskje ikke nok for oss - tross alt, hvis det er en stolpe midt på veien, kan vi ganske enkelt passere den. Hvilken avstand skal vi velge da? Centimeter? Millimeter? Mindre er bedre!

I det virkelige livÅ måle avstander til nærmeste millimeter er mer enn nok. Men matematikere streber alltid etter perfeksjon. Derfor ble konseptet oppfunnet uendelig liten, det vil si at den absolutte verdien er mindre enn et hvilket som helst tall vi kan navngi. For eksempel sier du: en trilliondel! Hvor mye mindre? Og du deler dette tallet på - og det blir enda mindre. Og så videre. Hvis vi vil skrive at en mengde er uendelig, skriver vi slik: (vi leser «x har en tendens til null»). Det er veldig viktig å forstå at dette tallet ikke er lik null! Men veldig nærme det. Dette betyr at du kan dele på det.

Konseptet motsatt til infinitesimal er uendelig stort (). Du har sikkert allerede kommet over det da du jobbet med ulikheter: dette tallet er modulo større enn noe tall du kan tenke deg. Hvis du kommer opp med det størst mulige tallet, multipliserer du det med to og du får et enda større tall. Og uendeligheten er enda større enn det som skjer. Faktisk er det uendelig store og det uendelig små det motsatte av hverandre, det vil si ved, og omvendt: at.

La oss nå gå tilbake til veien vår. Den ideelt beregnede helningen er helningen beregnet for et uendelig lite segment av banen, det vil si:

Jeg legger merke til at med en uendelig forskyvning vil høydeendringen også være uendelig. Men la meg minne deg på at infinitesimal ikke betyr lik null. Hvis du deler uendelige tall med hverandre, kan du få et helt ordinært tall, for eksempel . Det vil si at en liten verdi kan være nøyaktig ganger større enn en annen.

Hva er alt dette til for? Veien, brattheten... Vi skal ikke på bilrally, men vi underviser i matematikk. Og i matematikk er alt nøyaktig det samme, bare kalt annerledes.

Konseptet avledet

Den deriverte av en funksjon er forholdet mellom økningen av funksjonen og økningen av argumentet for en uendelig inkrement av argumentet.

Inkrementelt i matematikk kaller de endring. I hvilken grad argumentet () endres når det beveger seg langs aksen kalles argumentøkning og er betegnet hvor mye funksjonen (høyden) har endret seg når man beveger seg en avstand fremover langs aksen funksjonsøkning og er utpekt.

Så den deriverte av en funksjon er forholdet til når. Vi betegner den deriverte med samme bokstav som funksjonen, bare med et primtall øverst til høyre: eller ganske enkelt. Så la oss skrive den deriverte formelen ved å bruke disse notasjonene:

Som i analogien med veien, her når funksjonen øker, er den deriverte positiv, og når den avtar, er den negativ.

Er det mulig for den deriverte å være lik null? Sikkert. For eksempel, hvis vi kjører på en flat horisontal vei, er brattheten null. Og det er sant, høyden endres ikke i det hele tatt. Slik er det med den deriverte: den deriverte av en konstant funksjon (konstant) er lik null:

siden økningen av en slik funksjon er lik null for en hvilken som helst.

La oss huske eksempelet på en bakketopp. Det viste seg at det var mulig å arrangere endene av segmentet langs forskjellige sider fra toppen, slik at høyden i endene er den samme, det vil si at segmentet er parallelt med aksen:

Men store segmenter- et tegn på unøyaktig måling. Vi vil heve segmentet vårt opp parallelt med seg selv, så vil lengden reduseres.

Til slutt, når vi er uendelig nær toppen, vil lengden på segmentet bli uendelig liten. Men samtidig forble den parallelt med aksen, det vil si at forskjellen i høyder i endene er lik null (den pleier ikke, men er lik). Så den deriverte

Dette kan forstås slik: når vi står helt øverst, endrer en liten forskyvning til venstre eller høyre høyden vår ubetydelig.

Det er også en rent algebraisk forklaring: til venstre for toppunktet øker funksjonen, og til høyre reduseres den. Som vi fant ut tidligere, når en funksjon øker, er den deriverte positiv, og når den avtar, er den negativ. Men den endrer seg jevnt, uten hopp (siden veien ikke endrer helningen kraftig noe sted). Derfor, mellom negativ og positive verdier det må definitivt være. Det vil være der funksjonen verken øker eller minker - ved toppunktet.

Det samme gjelder for trauet (området der funksjonen til venstre avtar og til høyre øker):

Litt mer om økninger.

Så vi endrer argumentet til størrelsesorden. Vi endrer fra hvilken verdi? Hva har det (argumentet) blitt til nå? Vi kan velge hvilket som helst punkt, og nå skal vi danse fra det.

Tenk på et punkt med en koordinat. Verdien av funksjonen i den er lik. Så gjør vi det samme trinnet: vi øker koordinaten med. Hva er argumentet nå? Meget lett: . Hva er verdien av funksjonen nå? Der argumentet går, gjør også funksjonen: . Hva med funksjonsøkning? Ikke noe nytt: Dette er fortsatt beløpet som funksjonen har endret seg med:

Øv på å finne trinn:

1. Finn økningen til funksjonen på et punkt når økningen av argumentet er lik.
2. Det samme gjelder funksjonen på et punkt.

Løsninger:

På forskjellige punkter med samme argumentøkning vil funksjonen inkrement være forskjellig. Dette betyr at den deriverte på hvert punkt er forskjellig (vi diskuterte dette helt i begynnelsen - brattheten til veien er forskjellig på forskjellige punkter). Derfor, når vi skriver en derivert, må vi indikere på hvilket tidspunkt:

Power funksjon.

En potensfunksjon er en funksjon der argumentet til en viss grad er (logisk, ikke sant?).

Dessuten - i noen grad: .

Det enkleste tilfellet er når eksponenten er:

La oss finne dens deriverte på et punkt. La oss huske definisjonen av et derivat:

Så argumentasjonen endres fra til. Hva er økningen av funksjonen?

Inkrement er dette. Men en funksjon til enhver tid er lik argumentet. Derfor:

Den deriverte er lik:

Den deriverte av er lik:

b) Vurder nå den kvadratiske funksjonen (): .

La oss nå huske det. Dette betyr at verdien av økningen kan neglisjeres, siden den er uendelig liten, og derfor ubetydelig på bakgrunn av det andre begrepet:

Så vi kom opp med en annen regel:

c) Vi fortsetter den logiske rekken: .

Dette uttrykket kan forenkles på forskjellige måter: åpne den første parentesen ved å bruke formelen for forkortet multiplikasjon av kuben av summen, eller faktoriser hele uttrykket ved å bruke formelen for forskjellen av terninger. Prøv å gjøre det selv ved å bruke en av de foreslåtte metodene.

Så jeg fikk følgende:

Og igjen la oss huske det. Dette betyr at vi kan neglisjere alle termer som inneholder:

Vi får: .

d) Lignende regler kan oppnås for store makter:

e) Det viser seg at denne regelen kan generaliseres for en potensfunksjon med en vilkårlig eksponent, ikke engang et heltall:

(2)

Regelen kan formuleres med ordene: "graden fremføres som en koeffisient, og deretter reduseres med ."

Vi vil bevise denne regelen senere (nesten helt på slutten). La oss nå se på noen få eksempler. Finn den deriverte av funksjonene:

1. (på to måter: ved formel og ved å bruke definisjonen av derivert - ved å beregne økningen av funksjonen);

1. . Tro det eller ei, dette er en kraftfunksjon. Hvis du har spørsmål som "Hvordan er dette? Hvor er graden?", husk emnet ""!
   Ja, ja, roten er også en grad, bare brøk: .
   Dette betyr at kvadratroten vår bare er en potens med en eksponent:
   .
   Vi ser etter den deriverte ved å bruke den nylig lærte formelen:

   Hvis det på dette tidspunktet blir uklart igjen, gjenta emnet ""!!! (omtrent en grad med negativ eksponent)

2. . Nå eksponenten:

   Og nå gjennom definisjonen (har du glemt ennå?):
   ;
   .
   Nå, som vanlig, neglisjerer vi begrepet som inneholder:
   .

3. . Kombinasjon av tidligere saker: .

Trigonometriske funksjoner.

Her skal vi bruke ett faktum fra høyere matematikk:

Med uttrykk.

Du vil lære beviset i ditt første år på instituttet (og for å komme dit må du bestå Unified State Exam godt). Nå skal jeg bare vise det grafisk:

Vi ser at når funksjonen ikke eksisterer - kuttes punktet på grafen ut. Men jo nærmere verdien, desto nærmere er funksjonen. Dette er det som "måler".

I tillegg kan du sjekke denne regelen ved hjelp av en kalkulator. Ja, ja, ikke vær sjenert, ta en kalkulator, vi er ikke på Unified State Exam ennå.

Så, la oss prøve: ;

Ikke glem å bytte kalkulatoren til Radians-modus!

etc. Vi ser at jo mindre, jo nærmere er verdien av forholdet.

a) Vurder funksjonen. Som vanlig, la oss finne økningen:

La oss gjøre forskjellen på sinus til et produkt. For å gjøre dette bruker vi formelen (husk emnet ""): .

Nå den deriverte:

La oss gjøre en erstatning: . Så for infinitesimal er det også infinitesimal: . Uttrykket for har formen:

Og nå husker vi det med uttrykket. Og også, hva om en uendelig mengde kan neglisjeres i summen (det vil si at).

Så vi får følgende regel: den deriverte av sinus er lik cosinus:

Dette er grunnleggende ("tabellform") derivater. Her er de i en liste:

Senere vil vi legge til noen flere til dem, men disse er de viktigste, siden de brukes oftest.

Øve på:

1. Finn den deriverte av funksjonen i et punkt;
2. Finn den deriverte av funksjonen.

Løsninger:

1. La oss først finne den deriverte i generelt syn, og erstatte deretter verdien:
   ;
   .
2. Her har vi noe lignende strømfunksjon. La oss prøve å bringe henne til
   normal visning:
   .
   Flott, nå kan du bruke formelen:
   .
   .
3. . Eeeeeee.....Hva er dette????

Ok, du har rett, vi vet ennå ikke hvordan vi finner slike derivater. Her har vi en kombinasjon av flere typer funksjoner. For å jobbe med dem, må du lære noen flere regler:

Eksponent og naturlig logaritme.

Det er en funksjon i matematikk hvis deriverte for en hvilken som helst verdi er lik verdien av selve funksjonen på samme tid. Det kalles "eksponent", og er en eksponentiell funksjon

Grunnlaget for denne funksjonen er en konstant - den er uendelig desimal, det vil si et irrasjonelt tall (som f.eks.). Det kalles "Euler-nummeret", og det er derfor det er angitt med en bokstav.

Så, regelen:

Veldig lett å huske.

Vel, la oss ikke gå langt, la oss umiddelbart vurdere den inverse funksjonen. Hvilken funksjon er inversen til eksponentialfunksjonen? Logaritme:

I vårt tilfelle er basen tallet:

En slik logaritme (det vil si en logaritme med en base) kalles "naturlig", og vi bruker en spesiell notasjon for den: vi skriver i stedet.

Hva er det lik? Selvfølgelig, .

Den deriverte av den naturlige logaritmen er også veldig enkel:

Eksempler:

1. Finn den deriverte av funksjonen.
2. Hva er den deriverte av funksjonen?

Svar: Utstiller og naturlig logaritme- funksjoner er unikt enkle når det gjelder derivater. Eksponentielle og logaritmiske funksjoner med en hvilken som helst annen base vil ha en annen derivert, som vi vil analysere senere, etter at vi har gått gjennom reglene for differensiering.

Regler for differensiering

Regler for hva? Igjen en ny periode, igjen?!...

Differensiering er prosessen med å finne den deriverte.

Det er alt. Hva annet kan du kalle denne prosessen med ett ord? Ikke derivert... Matematikere kaller differensialet det samme inkrementet til en funksjon ved. Dette begrepet kommer fra det latinske differentia - forskjell. Her.

Når vi utleder alle disse reglene, vil vi bruke to funksjoner, for eksempel og. Vi trenger også formler for trinnene deres:

Det er 5 regler totalt.

Konstanten tas ut av det deriverte tegnet.

Hvis - et konstant tall (konstant), da.

Selvfølgelig fungerer denne regelen også for forskjellen: .

La oss bevise det. La det være, eller enklere.

Eksempler.

Finn de deriverte av funksjonene:

1. på et tidspunkt;
2. på et tidspunkt;
3. på et tidspunkt;
4. på punktet.

Løsninger:

1. (den deriverte er den samme på alle punkter, siden det er en lineær funksjon, husker du?);

Derivat av produktet

Alt er likt her: la oss gå inn ny funksjon og finn økningen:

Derivat:

Eksempler:

1. Finn de deriverte av funksjonene og;
2. Finn den deriverte av funksjonen i et punkt.

Løsninger:

Derivert av en eksponentiell funksjon

Nå er kunnskapen din nok til å lære hvordan du finner den deriverte av en hvilken som helst eksponentiell funksjon, og ikke bare eksponenter (har du glemt hva det er ennå?).

Så, hvor er et tall.

Vi kjenner allerede den deriverte av funksjonen, så la oss prøve å redusere funksjonen vår til en ny base:

Til dette vil vi bruke enkel regel: . Deretter:

Vel, det fungerte. Prøv nå å finne den deriverte, og ikke glem at denne funksjonen er kompleks.

Skjedd?

Her, sjekk deg selv:

Formelen viste seg å være veldig lik den deriverte av en eksponent: som den var, forblir den den samme, bare en faktor dukket opp, som bare er et tall, men ikke en variabel.

Eksempler:
Finn de deriverte av funksjonene:

Svar:

Dette er bare et tall som ikke kan beregnes uten en kalkulator, det vil si at det ikke kan skrives ned mer i enkel form. Derfor lar vi det stå i denne formen i svaret.

Derivert av en logaritmisk funksjon

Det er likt her: du kjenner allerede den deriverte av den naturlige logaritmen:

Derfor, for å finne en vilkårlig logaritme med en annen base, for eksempel:

Vi må redusere denne logaritmen til basen. Hvordan endrer du basen til en logaritme? Jeg håper du husker denne formelen:

Først nå vil vi skrive i stedet:

Nevneren er ganske enkelt en konstant (et konstant tall, uten en variabel). Deriverten oppnås veldig enkelt:

Derivater av eksponentielle og logaritmiske funksjoner finnes nesten aldri i Unified State Exam, men det vil ikke skade å kjenne dem.

Derivat av en kompleks funksjon.

Hva er en "kompleks funksjon"? Nei, dette er ikke en logaritme, og ikke en arctangent. Disse funksjonene kan være vanskelige å forstå (selv om du synes logaritmen er vanskelig, les emnet "Logarithms" så går det bra), men fra et matematisk synspunkt betyr ikke ordet "kompleks" "vanskelig".

Se for deg et lite transportbånd: to personer sitter og gjør noen handlinger med noen gjenstander. For eksempel pakker den første en sjokoladeplate inn i en innpakning, og den andre binder den med et bånd. Det blir slik sammensatt objekt: en sjokoladeplate pakket inn og bundet med et bånd. For å spise sjokoladebaren, må du gjøre de omvendte trinnene i motsatt rekkefølge.

La oss lage en lignende matematisk rørledning: først vil vi finne cosinus til et tall, og deretter kvadrere det resulterende tallet. Så vi får et tall (sjokolade), jeg finner dens cosinus (omslag), og så firer du det jeg har (bind det med et bånd). Hva skjedde? Funksjon. Dette er et eksempel på en kompleks funksjon: når vi, for å finne verdien, utfører den første handlingen direkte med variabelen, og deretter en andre handling med det som ble resultatet av den første.

Vi kan enkelt gjøre de samme trinnene i omvendt rekkefølge: først kvadrerer du det, og så ser jeg etter cosinus til det resulterende tallet: . Det er lett å gjette at resultatet nesten alltid vil være annerledes. Viktig funksjon komplekse funksjoner: når rekkefølgen av handlinger endres, endres funksjonen.

Med andre ord, en kompleks funksjon er en funksjon hvis argument er en annen funksjon: .

For det første eksemplet, .

Andre eksempel: (samme). .

Handlingen vi gjør sist vil bli kalt "ekstern" funksjon, og handlingen utført først - tilsvarende "intern" funksjon(dette er uformelle navn, jeg bruker dem kun for å forklare stoffet på et enkelt språk).

Prøv selv å finne ut hvilken funksjon som er ekstern og hvilken intern:

Svar:Å skille indre og ytre funksjoner er veldig likt å endre variabler: for eksempel i en funksjon

1. Hvilken handling vil vi utføre først? La oss først beregne sinusen, og først deretter kube den. Dette betyr at det er en intern funksjon, men en ekstern.
   Og den opprinnelige funksjonen er deres sammensetning: .
2. Internt: ; ekstern: .
   Eksamen:.
3. Internt: ; ekstern: .
   Eksamen:.
4. Internt: ; ekstern: .
   Eksamen:.
5. Internt: ; ekstern: .
   Eksamen:.

Vi endrer variabler og får en funksjon.

Vel, nå skal vi trekke ut sjokoladebaren vår og se etter derivatet. Prosedyren er alltid omvendt: først ser vi etter den deriverte av den ytre funksjonen, deretter multipliserer vi resultatet med den deriverte av den indre funksjonen. I forhold til det originale eksemplet ser det slik ut:

Et annet eksempel:

Så la oss til slutt formulere den offisielle regelen:

Algoritme for å finne den deriverte av en kompleks funksjon:

Det virker enkelt, ikke sant?

La oss sjekke med eksempler:

Løsninger:

1) Internt: ;

Ekstern: ;

2) Internt: ;

(Bare ikke prøv å kutte det nå! Ingenting kommer ut under kosinus, husker du?)

3) Internt: ;

Ekstern: ;

Det er umiddelbart klart at dette er en kompleks funksjon på tre nivåer: tross alt er dette allerede en kompleks funksjon i seg selv, og vi trekker også ut roten fra den, det vil si at vi utfører den tredje handlingen (vi legger sjokoladen i en innpakning og med et bånd i kofferten). Men det er ingen grunn til å være redd: vi vil fortsatt "pakke ut" denne funksjonen i samme rekkefølge som vanlig: fra slutten.

Det vil si at vi først differensierer roten, deretter cosinus, og først deretter uttrykket i parentes. Og så multipliserer vi det hele.

I slike tilfeller er det praktisk å nummerere handlingene. Det vil si, la oss forestille oss hva vi vet. I hvilken rekkefølge vil vi utføre handlinger for å beregne verdien av dette uttrykket? La oss se på et eksempel:

Jo senere handlingen utføres, jo mer "ekstern" vil den tilsvarende funksjonen være. Rekkefølgen av handlinger er den samme som før:

Her er hekkingen generelt 4-nivå. La oss bestemme handlingsrekkefølgen.

1. Radikalt uttrykk. .

2. Rot. .

3. Sinus. .

4. Firkantet. .

5. Sette alt sammen:

DERIVAT. KORT OM DE VIKTIGSTE TINGENE

Derivert av en funksjon- forholdet mellom økningen av funksjonen og økningen av argumentet for en uendelig økning av argumentet:

Grunnleggende derivater:

Regler for differensiering:

Konstanten tas ut av det deriverte tegnet:

Avledet av summen:

Avledet av produktet:

Derivat av kvotienten:

Derivert av en kompleks funksjon:

Algoritme for å finne den deriverte av en kompleks funksjon:

1. Vi definerer den "interne" funksjonen og finner dens deriverte.
2. Vi definerer den "eksterne" funksjonen og finner dens deriverte.
3. Vi multipliserer resultatene av det første og andre punktet.